 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Векторні випадкові величини
Розглянутий раніше теоретико-імовірнісний опис випадкових величин можна узагальнити на довільну сукупність випадкових величин: Приклад 2.4. Нехай маємо деяку інформаційну систему (ІС) з
Рис. 2.6. Приклад векторної випадкової величини
Тоді можливі значення напруги у момент часу Аналогічно, як і для одновимірної випадкової величини, вводиться багатовимірна функція сумісного розподілу імовірностей векторної випадкової величини.
тобто, за означенням, функція Сумісна функція розподілу неперервна зліва і неспадна по кожній змінній Окрім того багатовимірна сумісна функція розподілу має такі властивості: 1. 2. 3. Багатовимірна сумісна функція розподілу є симетричною функцією відносно своїх аргументів
де
де
Змішана похідна
називається Основні властивості 1. Вона є невід’ємною функцією
2. Багатовимірна сумісна щільність розподілу імовірностей, як і одновимірна, задовольняє умові нормування. Тобто
3. Якщо відома багатовимірна сумісна щільність розподілу імовірностей
4. На основі сумісної щільності розподілу імовірностей більшої розмірності завжди можна знайти сумісну щільність розподілу меншої розмірності, тобто
5. Для незалежних у сукупності випадкових величин
6. Імовірність того, що випадковий вектор
Для ілюстрації розглянемо рис. 2.7 з двовимірною щільністю розподілу імовірностей
Рис. 2.7. Двовимірна сумісна щільність розподілу імовірностей випадкового вектора в заштрихований на рисунку прямокутник
Поиск по сайту: |
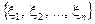 . Цю сукупність можна розглядати як випадковий вектор або випадкову точку у
. Цю сукупність можна розглядати як випадковий вектор або випадкову точку у  -вимірному евклідовому просторі з випадковими декартовими координатами
-вимірному евклідовому просторі з випадковими декартовими координатами  .
.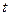 на кожному із
на кожному із 
 . На другому виході – значення випадкової величини
. На другому виході – значення випадкової величини 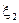 . І так далі. В цілому, можливі значення напруги на всіх
. І так далі. В цілому, можливі значення напруги на всіх  ,
, дорівнює імовірності події, яка полягає в тому, що випадкова величина
дорівнює імовірності події, яка полягає в тому, що випадкова величина  і випадкова величина
і випадкова величина 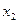 і т.д. до випадкової величини
і т.д. до випадкової величини  включно, тобто йде мова про перетин подій
включно, тобто йде мова про перетин подій  .
. .
. , де
, де 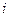 може дорівнювати будь-якому значенню із сукупності індексів
може дорівнювати будь-якому значенню із сукупності індексів  .
. .
.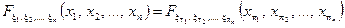 ,
,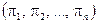 - будь-яка перестановка індексів
- будь-яка перестановка індексів  , (2.3)
, (2.3)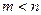 . Отже із розподілу більшої розмірності завжди можна отримати так званий маргінальний розподіл меншої розмірності за формулою (2.3). Обернене твердження у загальному випадку не вірне. Воно буде вірним лише для незалежних у сукупності випадкових величин
. Отже із розподілу більшої розмірності завжди можна отримати так званий маргінальний розподіл меншої розмірності за формулою (2.3). Обернене твердження у загальному випадку не вірне. Воно буде вірним лише для незалежних у сукупності випадкових величин  .
.
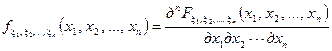
 .
. .
. , то відповідна сумісна функція розподілу векторної випадкової величини
, то відповідна сумісна функція розподілу векторної випадкової величини  .
.
 .
.
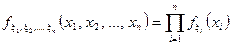 .
. , знаходиться за формулою:
, знаходиться за формулою: .
. . Імовірність попадання двовимірного випадкового вектора
. Імовірність попадання двовимірного випадкового вектора 
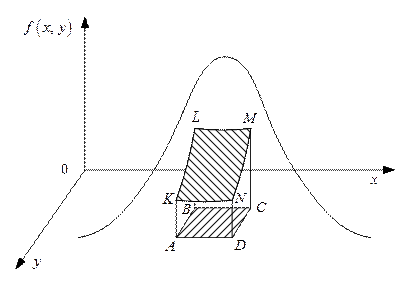
 дорівнює чисельно об’ємові шестигранної фігури
дорівнює чисельно об’ємові шестигранної фігури  і може бути обчислена за формулою
і може бути обчислена за формулою .
.