|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Нормальное распределение НСВ ⇐ ПредыдущаяСтр 3 из 3
Случайная величина Х, принимающая любые значения от
Нормальный закон распределения (также часто называемый законом Гаусса) имеет исключительное значение в теории вероятностей, т. к. это – наиболее часто встречающийся на практике закон распределения. Нормальное или близкое к нему распределение имеет огромное число случайных величин, встречающихся нам в жизни. Общим для их поведения является следующее: наиболее часто встречаются (наиболее вероятны) значения случайной величины, близкие к ее среднему арифметическому значению На рисунке слева приведен вид графиков
Характерная колоколообразная кривая, изображенная на рисунках, имеет специальное название — гауссиан (гауссова кривая). Параметр
не имеет аналитического выражения и вычисляется с помощью таблиц вспомогательной функции Ф( Рассмотрим наиболее часто встречающуюся задачу: расчет вероятности попадания значений Х в заданный интервал
1) Если то 2) Если то 3) Если то 4) Если то 5) Если то 6) Если то Пользуясь любым видом функции Ф(
Таким образом, практически достоверным событием (вероятность которого близка к 1) является попадание значений нормально распределенной величины на конечный промежуток от Кроме задачи вычисления вероятности попадания значений функции на интервал, встречается и обратная задача: по заданной вероятности установить интервал, симметричный относительно М(Х), на котором могут находиться значения случайной величины. Обычно задаваемую вероятность называют доверительной, обозначают Пусть Используя В таблице приведены значения
Поиск по сайту: |
 до
до  , имеет нормальное распределение с параметрами
, имеет нормальное распределение с параметрами  и
и 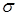 , если ее плотность распределения
, если ее плотность распределения 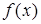 имеет вид:
имеет вид: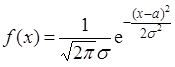 .
. . Чем сильнее отличаются значения
. Чем сильнее отличаются значения  от
от 

 ). (Вид графика этой функции приведен выше на рисунке справа). Эта функция имеет различные названия: интеграл (функция) Лапласа, интеграл вероятностей, функция ошибок, функция распределения (нормированного) нормального распределения. Эта функция может не только по-разному называться, но и приводиться в несколько различном виде, что следует учитывать, пользуясь ею.
). (Вид графика этой функции приведен выше на рисунке справа). Эта функция имеет различные названия: интеграл (функция) Лапласа, интеграл вероятностей, функция ошибок, функция распределения (нормированного) нормального распределения. Эта функция может не только по-разному называться, но и приводиться в несколько различном виде, что следует учитывать, пользуясь ею. :
: .
. ,
, .
. ,
, .
. ,
, .
. ,
, .
.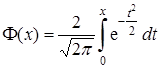 ,
, .
. ,
, .
. .
.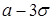 до
до  . Это обстоятельство позволяет успешно применять нормальный закон для описания поведения многих случайных величин, встречающихся в опыте, значения которых, конечно, меняются не от –
. Это обстоятельство позволяет успешно применять нормальный закон для описания поведения многих случайных величин, встречающихся в опыте, значения которых, конечно, меняются не от –  до +
до +  , а интервал, в котором с вероятностью
, а интервал, в котором с вероятностью  .
.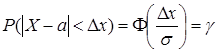 , откуда найдем, что
, откуда найдем, что 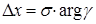 .
. при различных
при различных