 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Гипергеометрическое распределение ДСВСтр 1 из 3Следующая ⇒
Виды распределений случайных величин Равномерное распределение ДСВ Случайная величина
Найдем математическое ожидание и дисперсию равномерно распределенной случайной величины
Пример. Имеется связка из 5 ключей, из которых только один подходит к открываемому замку. Найти распределение случайной величины Очевидно,
Если Далее рассуждаем аналогично:
Биномиальное распределение ДСВ Случайная величина
Такое распределение имеет случайная величина
Пример. В корзине 50 шаров, из них 10 черных. Достают 5 шаров, причем выборка осуществляется с возвращением. Охарактеризовать случайную величину Х — число обнаруженных в выборке шаров черного цвета. Величина Х может принимать значения от 0 до 5, т. к. выборка проводится с возвращением, вероятность
Получим ряд распределения:
Найдем функцию распределения
Наивероятнейшее значение
Целым значением, удовлетворяющим этим двум неравенствам, является Гипергеометрическое распределение ДСВ Случайная величина Х имеет гипергеометрическое распределение, если
Такое распределение получается в следующей задаче. Имеется генеральная совокупность из Пример. Воспользуемся условием предыдущей задачи, считая, что выборка осуществляется без возвращения, и найдем закон распределения случайной величины Случайная величина
Составим ряд распределения
Как видим, вероятности отдельных значений Х несколько изменились по сравнению с их значениями, рассчитанными по формуле Бернулли. Числовые характеристики гипергеометрического распределения:
В данном примере Формулой для математического ожидания можно воспользоваться для оценки размера генеральной совокупности, если непосредственно подсчитать число объектов в ней затруднительно. Такая ситуация возникает, если нужно знать, например, число животных в популяции, обитающей на какой-либо территории, число птиц в стае, рыб в замкнутом водоеме и т. п. В этом случае метят
Поиск по сайту: |
 , принимающая целые значения от 1 до
, принимающая целые значения от 1 до 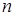 , имеет равномерное распределение, если
, имеет равномерное распределение, если .
.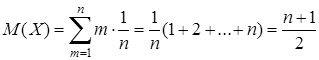 ;
;
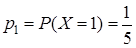 ;
; 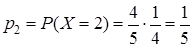 .
. , значит, опробованы 2 ключа. Данное событие представляет собой произведение двух событий: первый ключ не подошел, вероятность 4/5, второй подошел – вероятность 1/4.
, значит, опробованы 2 ключа. Данное событие представляет собой произведение двух событий: первый ключ не подошел, вероятность 4/5, второй подошел – вероятность 1/4. ;
; 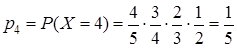 ;
; .
. .
.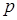 . Числовые характеристики биномиального распределения можно найти по формулам:
. Числовые характеристики биномиального распределения можно найти по формулам: .
. , где
, где 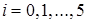 .
.

 :
: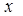
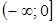

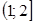





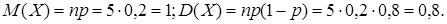
 ) определяется из неравенства
) определяется из неравенства или
или  .
. = 1. Значит,
= 1. Значит, 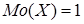 , что видно и из ряда распределения.
, что видно и из ряда распределения. .
. объектов, в числе которых находится
объектов, в числе которых находится  интересующих исследователей объектов. Из генеральной совокупности проводится выборка без возвращения объемом
интересующих исследователей объектов. Из генеральной совокупности проводится выборка без возвращения объемом 



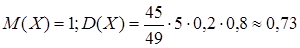 .
. . Зная
. Зная