 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Геометрическое распределение ДСВ
Случайная величина
Такое распределение имеет случайная величина, равная числу испытаний в схеме Бернулли до первого успеха (первого осуществления нужного события). Пример. Воспользуемся условием задачи из пунктов 32.2. и 32.3., но теперь уже будем проводить выборку с возвращением только до тех пор, пока не встретится черный шар. Составим ряд распределения случайной величины Х – количества сделанных попыток до появления черного шара. Величина Х может принимать бесконечное множество значений 0,1,2... Их вероятности вычисляются по формуле:
Вычислив по ней вероятности, составим ряд распределения:
Значения вероятностей являются членами геометрической прогрессии, использование свойств которой приводит к следующим формулам для числовых характеристик
Замечание. Формулы применимы, если число попыток не ограничено. В данном примере В некоторых задачах геометрическое распределение используется и для вычисления вероятностей общего числа сделанных попыток, причем число попыток может быть ограничено величиной
Распределение Пуассона ДСВ Случайная величина
где Числовые характеристики пуассоновского распределения:
Равномерное распределение НСВ Случайная величина
Функция распределения:
Графики функций
Числовые характеристики равномерного распределения:
Пример. Известно, что НСВ Воспользовавшись предыдущими формулами, составим систему:
У этой системы два решения:
Поиск по сайту: |
 имеет геометрическое распределение, если
имеет геометрическое распределение, если
 .
.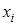
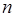


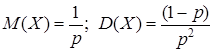 .
.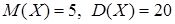 .
.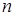 . В этом случае
. В этом случае 



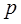
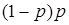

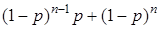
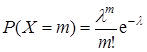 ,
, – параметр распределения, имеет смысл среднего числа наступлений события за единицу времени. Величины, которые подчиняются подобному распределению, были описаны в разделе.
– параметр распределения, имеет смысл среднего числа наступлений события за единицу времени. Величины, которые подчиняются подобному распределению, были описаны в разделе.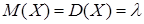 .
. , имеет равномерное распределение, если плотность распределения
, имеет равномерное распределение, если плотность распределения  имеет вид:
имеет вид: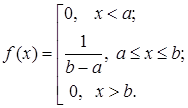
 .
. приведены на рисунках.
приведены на рисунках.
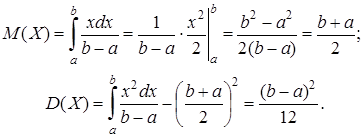
 ;
; 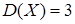 . Найти промежуток
. Найти промежуток 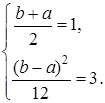
 и
и 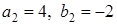 . Т.к. должно быть
. Т.к. должно быть 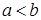 , то выбираем первую пару в качестве концов отрезка.
, то выбираем первую пару в качестве концов отрезка.