 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 5. Диференціальне числення ⇐ ПредыдущаяСтр 4 из 4
1. Диференціювання функцій від однієї змінної. 2. Дослідження функцій за допомогою похідних. 3. Економічний сенс похідної.
5.1. Диференціювання функцій від однієї змінної
Означення. Нехай y = f(x) ‑ деяка функція; x ‑ деяка точка з області визначення y=f(x) . Похідною функції y=f(x) у точці x називається границя відношення приросту функції до приросту аргументу, якщо приріст аргументу довільним чином прямує до нуля:
Використовують також позначення
Наведемо таблицю похідних від елементарних функцій:
C¢=0; x¢ =1; (xn)¢ =nxn-1 , у тому числі
(sinx)¢ = cosx; (cosx)¢ = - sinx;
Є такі правила обчислення похідних: (u+v)¢ = u¢ + v¢ ‑ похідна від суми; (uv)¢ =u¢v + uv¢ ‑ похідна від добутку;
[f(g(x))]¢ = f¢(g(x))×g¢(x) похідна від складної функції. Приклади. Обчислити похідну від функції y=f(x) (продиференціювати функцію y=f(x)): 1) f(x) = 3x2 + ex; f¢(x) = 3×2x + ex; 2) f(x) = 3e-2x + 4lgx; f¢(x) = 3) f(x) = f¢(x) =
4) f(x) = f¢(x) = 5) f(x) = sin2x = (sinx)2; f¢(x) = (2sinx)×(sinx)¢ =2sinx×cosx =sin2x; 6) f(x) = sinx2 = sin (x2); f¢(x) = (cos(x2))×(x2)¢ = 2xcosx2; 7) f¢(x)= (1/4)(1-sin3x)-3/4×(-cos3x)×3. Приклад. Обчислити другу похідну від функції y(x) = x3 + sinx: y¢¢(x) = (y¢(x))¢ = (x3+sinx) ¢¢ = = (3x2+cosx) ¢ =6x – sinx. Нагадаємо також, що функція y=f(x) називається диференційовною в точці x0 , якщо в цій точці існує похідна y¢=f¢(x). Функція, диференційовна в деякій точці (на деякому відрізку) є неперервною в цій точці (на цьому відрізку).
5.2. Дослідження функцій за допомогою похідних
Означення. Функція y=f(x) має мінімум (максимум) у точці x0 , якщо існує такий окіл точки x0 , що для всіх точок x¹x0 цього околу виконується нерівність f(x0)<f(x) (f(x0)<f(x)).
Рис. 5.1.
Функція, показана на рис. 5.1, має два мінімуми та три максимуми. Нагадаємо, що поняття мінімуму та максимуму об’єднані в термін “екстремум”. Теорема (необхідна умова існування екстремуму). Якщо диференційовна функція f(x) в точці x0 має екстремум, то в цій точці похідна f¢(x0) =0. Теорема. Якщо на деякому відрізку [a;b] похідна f¢(x) від деякої функції є додатною (від’ємною), то на цьому відрізку функція f(x) зростає (спадає) Теорема (перша достатня умова існування екстремуму). Якщо похідна f¢(x) від деякої диференційоної функції f(x) в точці x=x0 дорівнює нулю і при x<x0 похідна f¢(x)>0, а при x>x0 похідна f¢(x)<0, то точка x0 є точкою максимуму. Якщо ж похідна f¢(x) в деякому околі точки x0 змінює знак з від’ємного на додатний, то точка x0 є точкою мінімуму.
Теорема (друга достатня умова існування екстремуму). Якщо в точці x0 диференційовної функції y = f(x) перша похідна f¢(x)=0 , а друга f¢¢(x)<0 , то в цій точці є максимум (мінімум, якщо f¢¢(x)>0) . Поняття мінімуму та максимуму не треба плутати з поняттями найбільшого та найменшого значень функції на деякому інтервалі.
Зазначимо, що умова f¢(x)=0 не є достатньою для існування екстремуму функції y=f(x). Нехай y = f(x) ‑ деяка функція та (x0;y0) ‑ точка з області визначення цієї функції. Проведемо через точку (x0;y0) дотичну до кривої (рис. 5.2).
Рис. 5.2.
Рівняння цієї дотичної – це пряма y = f(x0) +f¢(x0)(x-x0) (5.2) Величина f¢(x0) = k = tga є нахилом кривої y=f(x) в точці x0 . Означення. Диференціалом від функції y=f(x) називається вираз dy=f¢(x)dx, де dx = Dx ‑ приріст аргументу (рис. 5.2). Приклад. Нехай y = ln(x2+1) . Тоді Приклад. Знайти екстремуми та інтервали зростання і спадання функції y = x3 – 6x2 +9x. Знаходимо похідну y¢ =3x2 – 12x +9. Розв’язуємо рівняння 3x2 – 12x +9=0 , звідки x1=1; x2=3. Досліджуємо знаки першої похідної
Точки x1=1 та x2=3 можна також дослідити згідно з другою достатньою умовою екстремуму: y²(x) = 6x – 12; y²(1) = - 6 < 0, отже, в точці x=1 функція y = x3 – 6x2 +9x досягає максимуму; y²(3) = 6 > 0, отже, в точці x=3 ця функція має мінімум. Означення. Функція f(x) називається випуклою (випуклою вверх) на відрізку [a;b] , якщо на цьому інтервалі її графік розташований нижче від її дотичної (рис. 5.3,а). Функція f(x) називається увігнутою (випуклою вниз), якщо на [a;b] цей графік розташований нижче від дотичної (рис. 5.3,б).
а x б x Рис. 5.3.
Теорема (достатня умова випуклості). Якщо у всіх точках інтервалу [a;b] друга похідна f²(x) двічі диференційовної функції y=f(x) є додатною f²(x)>0, то функція y=f(x) є увігнутою на [a;b] . Якщо f²(x)<0 , то функція y=f(x) випукла на інтервалі [a;b] . Означення. Точка x0, у якій функція y=f(x) змінює увігнутість на опуклість (або навпаки), називається точкою перегину функції y=f(x) (рис. 5.4). Теорема (достатня ознака існування точки перегину). Якщо в точці x0 існує перша похідна f¢(x) і f²(x)=0 , причому друга похідна f²(x) змінює знак, то точка x0 є точкою перегину функції y=f(x) (рис. 5.4).
Рис. 5.4.
Приклад. Знайти інтервали випуклості та увігнутості функції y = x3 ‑ 6x2 + 9x . Друга похідна y²(x)=6x-12 дорівнює нулю в точці x=2. Тому визначимо знаки цієї другої похідної на інтервалах (-∞;2) та (2;∞).
Отже, функція y(x) є випуклою на інтервалі (-∞;2), у точці x=2 має перегин, а на інтервалі (2;∞) увігнута.
Приклад. Дослідити властивості логістичної кривої (рис. 4.12). Логістичною функцією описують еволюцію продажу на ринку нового товару. Загальний вигляд логістичної функції (кривої) такий: При t=0 маємо y(0)= Знайдемо першу похідну від функції
Знайдемо другу похідну від y(t), тобто обчислимо
Розв’яжемо рівняння y²(t) = 0 на інтервалі t>0, тобто рівняння 0,01-0,1×0,5t = 0 , звідки 0,5t = 0,1; tlg0,5 = lg0,1; t(-lg2) = -1; t0 = 1/lg2 » 3,32. Отже, при t0=3,32 логістична крива має перегин. Значення y(t0) в точці перегину
На інтервалі 0<t<t0 логістична функція увігнута (кількість проданого товару залежно від часу зростає щораз швидше). Проте на нескінченному інтервалі t0<t функція є випуклою (кількість проданого товару хоча й зростає, проте це зростання уповільнюється).
Приклад. Витрати на споживання деяких товарів (другої потреби) залежно від доходу описує функція Торнквіста Похідна Друга похідна Отже, витрати на споживання y збільшуються зі зростанням доходу z, проте швидкість цього зростання зменшується (граничні витрати зменшуються). Обчислимо також Отже, витрати на споживання цього товару не можуть перевищити a.
Приклад. На інтервалі (0,1; 0,5) залежність розміру надходжень до бюджету y від ставки оподаткування x описує крива (функція) Лаффера (рис. 5.5):
Дослідимо цю функцію, обчисливши першу та другу похідні:
Рис. 5.5.
Легко бачити, що при x=0,3 похідна y¢(x)=0, причому друга похідна y²(x)>0 . Отже, ставка оподаткування x=0,3 = 30% в нашому прикладі дає найбільше надходження до бюджету. Із рівняння y²(x) = 0 знаходимо точки перегину кривої
5.3. Економічний сенс похідної
Покажемо, як деякі економічні показники (граничне значення, темп приросту та еластичність) обчислюютьза допомогою похідної. Означення (економічне). Граничним значенням My(x) показника y = y(x) називається приріст цього показника унаслідок додаткового збільшення аргументу x. Нехай Dx ‑ приріст цього аргументу, а Dy ‑ приріст показника. Тоді My(x) = y¢(x) . (5.3) Приклад. Випуск продукції Q залежно від затрат x описує функція Тоді граничний продукт Тепер
Q (випуск)
x (затрати) Рис. 5.6.
Приклад. Корисність U від споживання деякого блага x задана функцією U=U(x)= ln(1+x) (рис. 5.7). Тоді гранична корисність Зі зростанням кількості спожитих благ їхня гранична корисність зменшується.
x (кількість благ)
Рис. 5.7.
Означення (економічне). Темпом приросту Ty(t) величини y=y(t) називається відносна зміна значення y за деякий проміжок часу. Нехай час t змінився на проміжок Dt. Тоді При Dt®0 маємо Приклад. Зміну кількості населення деякої країни описує функція P = 100000000e0,02t. Тоді темп приросту цього населення
(протягом кожного наступного року кількість населення зростає на 2% по відношенню до попереднього). Означення (економічне). Еластичністю Ey(x) показника y = y(x) за аргументом x називається відношення відносної зміни цього показника до відносної зміни аргументу. Отже,
Приклад. Попит Q на деякий товар в залежності від його ціни p описує залежність
Q (величина попиту) Рис. 5.8.
Визначимо еластичніть цього попиту. Згідно з отриманою формулою
Поиск по сайту: |
 (5.1)
(5.1) .
. ;
; ;
; , у тому числі
, у тому числі  ;
; , у тому числі
, у тому числі  ;
; ;
;  ;
; ;
;  ;
; ;
;  ;
; ‑ похідна від частки;
‑ похідна від частки; ;
; ;
;
 ;
; ;
; ;
; ;
;
 y
y
 x0 x
x0 x


 y y=f(x)
y y=f(x)
 Dy
Dy
 dy
dy dx=Dx
dx=Dx a
a x0 x
x0 x .
.
 y y
y y



 y
y
 x0 x
x0 x . Дослідимо конкретну логістичну функцію вигляду
. Дослідимо конкретну логістичну функцію вигляду  .
. .
.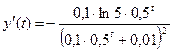 . Оскільки для всіх t вираз 0,5t є завжди додатним, то перша похідна y¢(x) ніколи не перетворюється в нуль, отже, логістична крива екстремумів не має.
. Оскільки для всіх t вираз 0,5t є завжди додатним, то перша похідна y¢(x) ніколи не перетворюється в нуль, отже, логістична крива екстремумів не має.



 .
. (a, b, c >0). Дослідимо цю функцію (рис. 4.13).
(a, b, c >0). Дослідимо цю функцію (рис. 4.13). завжди є додатнью на інтервалі z>0.
завжди є додатнью на інтервалі z>0. від’ємна.
від’ємна. .
. .
. ;
; .
. y
y


 50
50 0,3 x
0,3 x .
. . Якщо y=y(x) є неперервною фукцією від x, то, перейшовши до границі, отримуємо
. Якщо y=y(x) є неперервною фукцією від x, то, перейшовши до границі, отримуємо  , тобто
, тобто (рис. 5.6).
(рис. 5.6). .
. , отже зі збільшенням затрат граничний продукт зменшується.
, отже зі збільшенням затрат граничний продукт зменшується.





 dQ
dQ dx
dx
 . Похідна MU¢=U²(x)=
. Похідна MU¢=U²(x)=  .
. U (корисність)
U (корисність)

 dU
dU
 dx
dx
 .
. , тобто
, тобто  . (5.4)
. (5.4)
 . Перейшовши до границі при Dx®0, отримуємо
. Перейшовши до границі при Dx®0, отримуємо (5.5)
(5.5) (рис. 5.8).
(рис. 5.8). p (ціна)
p (ціна)
 Крива попиту
Крива попиту
 Dp
Dp
 DQ
DQ . Отже, зі збільшенням ціни на 1% попит на товар зменшиться на 2% . У разі зменшення ціни в 1,2 раза попит збільшиться в 2,4 раза.
. Отже, зі збільшенням ціни на 1% попит на товар зменшиться на 2% . У разі зменшення ціни в 1,2 раза попит збільшиться в 2,4 раза.