 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 1. Лінійна алгебраСтр 1 из 4Следующая ⇒
Частина 1
1. Матриці та вектори. 2. Визначники. 3. Системи лінійних алгебраїчних рівнянь.
1.1. Матриці та вектори. Означення. Матрицею розміром n×m називається прямокутна таблиця чисел
Означення. Матриці A=(aij) та B=(bij) називаються рівними (однаковими), якщо вони мають однакову кількість рядків та стовпців і всі їхні елементи, розташовані на однакових місцях, є рівними (тобто aij=bij для всіх значень i та j).
Означення. Сумою двох матриць A=(aij) та B=(bij) з однаковою кількістю рядків та стовпців називається матриця C=A+B, де cij=aij+bij (i=1,…,m; j=1,…,n). (1.1) Означення. Добутком матриці A=(aij) на число k називається матриця B=k×A вигляду B=k×A=(k×aij). Матриця називається квадратною, якщо кількість її рядків співпадає із кількістю стовпців (n=m). Означення. Квадратна матриця E=(eij) називається одиничною, якщо
тобто ця матриця має вигляд
Означення. Матриця O називається нульовою, якщо всі її елементи є нулями: Означення. Добутком матриці
Приклади. 1. Нехай Тоді 2. Нехай, крім того,
Тоді D×C - не має сенсу,
Зазначимо, що в останньому прикладі А×В ¹ В×А . Виконуються такі властивості додавання та множення матриць: Е×А = А×Е = А (властивість множення на одиничну матрицю); О×А = А×О = О (властивість множення на нульову матрицю); k×O = O×k = O A+O = O+A =A; a(bA) = (ab)A; (Aa)b = A(ab); A+B = B+A (комутативна властивість додавання); A+(B+C)=(A+B)+C (асоціативна властивість додавання); (a+b)A = aA+bA; a(AB) =(aA)B; (A+B)C = AC+BC ; C(A+B) = CA+CB. Означення. Матрицею AT, транспонованою до матриці Виконуються такі властивості: (AB)T = BTAT; (aA+bB)T = aAT+bBT; (AT)T = A.
Частковим випадком матриці є вектор (упорядкована послідовність чисел). Розрізняють вектор-рядок (матрицю-рядок) Добуток матриці на вектор обчислюється за загальним означенням множення матриць:
Приклад. Для виготовлення виробів W1 та W2 потрібні вузли v1 та v2. Для виготовлення цих вузлів, в свою чергу, відповідно, потрібні деталі d1, d2 та d3 у кількостях, що наведені у таблицях:
Обчислити кількість деталей, що потрібні для виготовлення кожного із виробів W1 та W2.
На основі аналізу цих таблиць бачимо, що шукана кількість деталей облислюється як добуток матриць
Отриманий результат такий:
Зокрема, для виготовлення виробу W2 потрібно 12 деталей d3. Приклад. Нарахувати заробітну плату, яку потрібно виплатити на кожне замовлення, якщо вхідна інформація задана у таблицях: Таблиця A
Таблиця B
Таблиця C
Помноживши матрицю B на матрицю A, отримуємо затрати часу на робочих місцях щодо кожного замовлення:
Справді, Перемноживши отриману матрицю на вектор (матрицю-стовпець) C, обчислимо витрати на зарплату щодо кожного із замовлень:
Отже, витрати на зарплату обчислюються як добуток матриць:
Комплектуюча Комплектуюча Деталь Деталь
D1 D2 D1 D2
Рис. 1.1. Визначити загальне входження кожної з деталей D1 та D2 у виробі. Побудуємо відповідні матриці. Матриця входжень деталей у комплектуючих: Безпосереднє входження деталей у виробі – це вектор Тоді загальну кількість деталей D1 та D2 у виробі обчислюють за формулою
Отже, для виготовлення одного виробу потрібно 30 деталей D1 та 42 деталі D2 .
Означення. Нехай A=(aij)i=1,…,n;j=1,…,n ‑ квадратна матриця. Оберненою до неї матрицею A-1 називається матриця, для якої має місце A×A-1=A-1×A=E . Якщо обернена до A матриця існує, то (A-1)-1=A. Приклад. Нехай Справді,
За допомогою оберненої матриці можна розв’язувати системи лінійних рівнянь, оскільки запис
Розв’язок
Відшукання оберненої матриці досить складна математична задача. Проте дії над матрицями реалізовані у багатьох комп’ютерних системах. Зокрема, в системі EXCEL обчислення оберненої матриці реалізується за допомогою так званої функції масиву MINVERSE, а множення матриць –за допомогою функції масиву MMULT (зазначимо, що функція масиву, на відміну від звичайної функції, вводиться одночасним натисканням трьох клавіш – Shift, Ctrl та Enter). 1.2. Визначники
Означення. Визначником (детермінантом) матриці другого порядку
Означення. Визначником (детермінантом) матриці третього порядку
Приклади:
Означення. Визначником квадратної матриці A розміру n×n називається число
Сума обчислюється за всіма перестановками (i1,…,in). Величина inv(i1,…,in) це кількість інверсій перестановки (i1,…,in), тобто кількість пар (ik,im) таких, що ik>im , проте ik розташоване лівіше від im . Легко перевірити, що означення визначника другого та третього порядку задовольняє загальне означення.
Множина визначників задовольняє такі властивості: 1. У разі транспонування матриці значення визначника не змінюється:
2. У випадку перестановки двох довільних рядків (або двох довільних стовпців) знак визначника змінюється на протилежний:
3. Якщо всі елементи одного рядка (стовпця) матриці є пропорційними до елементів другого рядка (стовпця) цієї матриці, то її визначник дорівнює нулю:
є вдвічі більшими від елементів першого. 4. Якщо всі елементи рядка (стовпця) помножити на якесь число, то визначник теж помножиться на це ж число:
5. Якщо до елементів деякого рядка (стовпця) додати елементи іншого рядка (стовпця), помножені на довільне число, то значення визначника не зміниться:
Означення. Мінором Mij елемента aij визначника Приклад. У визначнику Означення. Алгебраїчним доповненням Aij елемента aij називається його мінор, узятий зі знаком (+) або (-) так: якщо сума (i+j) номерів рядка i та стовпця j є парною, то потрібно взяти знак (+), якщо ж ця сума непарна – то знак (-).
Для визначника довільного порядку виконується така Теорема. Визначник дорівнює сумі добутків елементів довільного рядка (стовпця) на алгебраїчні доповнення цих елементів. Зокрема,
Приклад. Обчислити визначник Згідно з означенням D=2×8×5+5×0×1+3×3×(-2)-1×8×(-2)-5×3×5-2×0×3=3. За теоремою (розкладаємо визначник за елементами другого рядка) отримуємо той самий результат: D = a21A21+a22A22+a23A23 = a21(-M21)+a22M22+a23(-M23) = = Таким способом обчислення визначників високих порядків можна послідовно зводити до відшукання визначників щораз менших порядків. Зазначимо також, що функція MDETERM системи EXCEL дає змогу автоматизувати обчислення визначників досить високих порядків.
Розглянемо довільну (не обов’язково квадратну) матрицю A . Рангом r(A) цієї матриці називається найвищий порядок її мінора, що не дорівнює нулю. Приклад. Матриця
Розглянемо систему векторів
Якщо ж із рівності Приклад. Система векторів
Приклад. Система векторів
виконується тільки при k1 = k2 = 0 . Легко бачити, що при m > n система векторів завжди є лінійно залежною. Приклад. Нехай
Рис. 1.2 Пропорційні вектори завжди лінійно залежні. Приклад. Нехай
Нехай задана деяка система векторів - ця підсистема лінійно незалежна; - кількість елементів k цієї підсистеми є максимально можливою.
Приклад. Базисом системи
Приклад. Базисом тривимірного простору R3 є система векторів {(1;0;0;), (0;1;0), (0;0;1)} .
Означення. Нехай
Приклад. Обчислити власні значення матриці Будуємо рівняння для відшукання власних чисел: Розв’язуємо це рівняння: (1-l)×(4-l)-(-1)×2 = 0; l2 -5l+6=0; l1 = 2; l2 = 3. Означення. Квадратна матриця називається додатно визначеною, якщо всі її власні числа є додатними. Теорема. Квадратна матриця a11 > 0;
. . . . . . . . .
Приклад. Матриця a11 = 1 > 0;
Означення. Власним (характеристичним) вектором матриці A називається вектор Приклад. Вектори
3. Системи лінійних алгебраїчних рівнянь
Розглянемо систему двох рівнянь з двома невідомими
Кожне з цих рівнянь задає деяку пряму на площині. Позначимо основну матрицю цієї системи через Можливі три такі випадки: - ранг матриці r(A)=2. Вектори (a1;b1;c1) та (a2;b2;c2), отже, є лінійно незалежними і система має єдиний розв’язок (x0;y0). Геометрично маємо дві прямі на площині, які перетинаються в одній точці; - ранг розширеної матриці r(B)=2, а ранг основної r(A)=1. Вектори (a1;b1;c1) та (a2;b2;c2) є лінійно незалежними, а вектори (a1;b1) та (a2;b2) – лінійно залежними. Рівняння системи це дві паралельні прямі., Отже, система не має розв’язків; - ранг як основної, так і розширеної матриці дорівнює одиниці: r(A)=r(B)=1. Вектори (a1;b1;c1) та (a2;b2;c2) є лінійно залежними. Геометрично маємо дві прямі, які збігаються. Система має безліч розв’язків.
Розглянемо тепер систему трьох рівнянь з трьома невідомими
Кожне рівняння цієї системи задає деяку площину в просторі. Можливі такі випадки: - усі три площини перетинаються в одній точці (x0;y0;z0). Ранг r(A)=3. Система має єдиний розв’язок (x0;y0;z0); - усі три площини перетинаються по одній прямій (при цьому площини можуть збігатися). Ранг r(A)<3 та ранг r(B)<3. Система має безліч розв’язків; - хоча б дві площини є паралельними між собою (r(A)<3 та r(B)=3). Система розв’язків не має. Розглянемо систему двох рівнянь з трьома невідомими
Можливі лише такі випадки: - дві площини, задані цими рівняннями, паралельні. Це є тоді, коли ранг звичайної (основної) матриці r(A)=1, а ранг розширеної – r(B)=2. Система розв’язків не має; - обидві площини співпадають. Вектори (a1;b1;c1;d1) та (a2;b2;c2;d2) лінійно залежні. Система має безліч розв’язків; - площини перетинаються по прямій. Ранги обох матриць r(A)=r(B)=2. Ці ранги є меншими від кількості невідомих системи. Система, отже, має безліч розв’язків. Зазначимо, що множиною розв’язків у другому випадку є площина, а в третьому – пряма. Тому розв’язати систему двох рівнянь з трьома невідомими ‑ означає описати аналітично множину всіх розв’язків. Приклад. Розв’язати систему Перенесемо змінну x у праву частину: Помножимо перше рівняння на -2 і додамо до другого: 4z = -28 Помножимо перше рівняння на 2 і додамо до другого: -8y = 32-4x Розв’язуючи отриману систему y = (1/2)x-4 ; z = -7. Отже, загальний розв’язок початкової системи має вигляд {(x; -4+0,5x;7)|xÎR}. Надаючи параметру x різних значень, ми отримуємо конкретні розв’язки. Наприклад, при x=1 розв’язком є трійка чисел (1; -3,5; -7), при x=0 – (0; -4; -7) , а при x=5 – (10; 1; -7). Трійку чисел (2; 2; 2) не можна отримати при жодному значенні параметра, отже, розв’язком системи вона не є.
Розглянемо методи розв’язування систем n лінійних рівнянь з nневідомими
Одним із способів є використання оберненої матриці:
Розглянемо також правило Крамера. Нехай D ‑ визначник матриці Введемо позначення
Виконується така теорема: Якщо D¹0, то система
Якщо D=0 і в множині {D1,…,Dn} є ненульові елементи, то система рівнянь розв’язків не має. Якщо ж D=D1=…Dn=0 , то система має безліч розв’язків. Приклад.
Тут
Отже, x1=81/27=3; x2=(-108)/27=-4; x3=(-27)/27=-1; x4=27/27=1.
У шкільному курсі математики вивчають метод послідовного вилучення невідомих (метод Гауса). Ми наведемо модифікований метод вилучення невідомих – так званий метод Жордана-Гауса. Розглянемо схему Жордана-Гауса на прикладі розв’язування конкретної системи яку у матричному вигляді записують так: Початкова таблиця має такий вигляд:
Числа -2 та -3 ‑ це елементи другого та третього рядка (взяті з протилежним знаком), які розташовані в тому стовпці, де в першому рядку є число 1. Множимо перший рядок на числа -2 та -3 й отримуємо, відповідно, вектори (-2; -4; 6; 12) та (-3; -6; 9; 18). Додаємо ці вектори до другого і третього рядків:
Ділимо всі елементи другого рядка на -5, роблячи діагональний елемент таблиці одиничним:
Розпочинаємо наступний етап методу. Множимо другий рядок на -2 та на 4 й отримуємо вектори (0; -2; 14/5; 22/5) і (0; 4;-28/5;-44/5). Додаємо ці вектори до першого та третього рядків:
і робимо ще один діагональний елемент одиницею (ділимо на 22/5):
На останньому кроці множимо третій рядок на 1/5 та 1/7 і додаємо утворені вектори (0;0;1/5;3/5) і (0;0;7/5;21/5) до першого та другого рядка:
Якщо під час обчислень у схемі Жордана-Гауса деякий рядок повністю стає нульовим ( 0 0 0 | 0 ), то це є ознакою того факту, що система має безліч розв’язків. Якщо ж цей рядок стає нульовим за винятком вільного члена ( 0 0 0 | bi¹0 ), то система розв’язків не має.
Приклад. Модель міжгалузевого балансу Леонтьєва. Нехай у деякій державі є три галузі господарства: промисловість, сільське господарство та виготовлення ЕОМ. Нехай x1, x2, x3 ‑ обсяги виробництва у цих галузях. Нехай також y1, y2 y3 ‑ обсяги кінцевого виробництва (виробництва на продаж, виробництва без внутрішнього споживання) цих галузей (рис. 1.3).
y1 x1 x2
a31x1 a13x3 a23x3 a32x2
Виготовлення
x3 y3
a33x3 Рис. 1.3. Нехай aij ‑ кількість одиниць продукції i-ої галузі, яка йде на виробництво однієї одиниці продукції j-ої галузі. Зокрема, кожна одиниця продукції сільськогосподарської галузі (галузі номер 2) використовує a12 одиниць продукції промисловості (галузі номер 1) та a32 одиниць продукції галузі, яка виготовляє комп’ютери. Тоді сільське господарство в цілому використовує для випуску своєї продукції a12x2 одиниць продукції промисловості та a32x2 одиниць продукції комп’ютерної галузі. Крім того, сільське господарство витрачає a22x2 одиниць власної продукції (наприклад, відгодівля худоби потребує певних затрат кормів). Отже, для другої галузі маємо таке рівняння балансу: x1 = a11x1 + a12x2 + a13x3 + y1 Записавши аналогічні рівняння для кожної із галузей, отримуємо систему лінійних рівнянь:
Цю систему для випадку n змінних записують також у вигляді
та в матричному вигляді
Побудована система міжгалузевого балансу (модель Леонтьєва) дає змогу за обсягами виробництва в окремих галузях контролювати їхній кінцевий продукт та навпаки. Із формули (1.8) випливає, що вектор кінцевої продукції в моделі Леонтьєва визначається формулою
а вектор загального випуску –
Поиск по сайту: |

 ,
, .
. .
. на матрицю
на матрицю  називається матриця
називається матриця  , елементи якої обчислюються за формулою
, елементи якої обчислюються за формулою (1.2)
(1.2)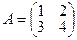 та
та  .
. ,
,  ,
,  .
. та
та  .
. ,
,
 .
. та вектор- стовпець (матрицю-стовпець)
та вектор- стовпець (матрицю-стовпець)  .
.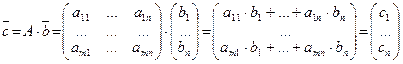 ,
,
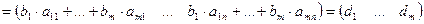 .
. .
. .
. .
. Приклад. Входження деталей та комплектуючих у деякий виріб показане на рисунку 1.1 :
Приклад. Входження деталей та комплектуючих у деякий виріб показане на рисунку 1.1 :

 Виріб
Виріб


 4 3 10 15
4 3 10 15
 K1 K2 D1 D2
K1 K2 D1 D2
 2 3 4 5
2 3 4 5

 . Тут рядки відповідають деталям, а стовпці комплектуючим.
. Тут рядки відповідають деталям, а стовпці комплектуючим. , а входження комплектуючих у виробі – вектор
, а входження комплектуючих у виробі – вектор  .
. .
. . Тоді
. Тоді 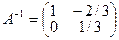 .
. ,
, .
.
 , де
, де 

 системи
системи  ,
, , (1.3)
, (1.3) .
. називається число
називається число  .
. називається число D(A)=
називається число D(A)= 

 ;
; .
. (1.4)
(1.4) .
. .
. , оскільки елементи третього рядка
, оскільки елементи третього рядка .
. .
. називається визначник розміру (n-1)×(n-1) , який утворюється з визначника
називається визначник розміру (n-1)×(n-1) , який утворюється з визначника  визначники другого порядку
визначники другого порядку  є відповідно мінорами елементів a1, b1 та c1.
є відповідно мінорами елементів a1, b1 та c1. .
. =(-3)×31+8×12+(-0)×1 = 3
=(-3)×31+8×12+(-0)×1 = 3 має три мінори третього поряду (всі з яких дорівнюють нулю), дев’ять мінорів другого порядку (з яких деякі дорівнюють нулю, а деякі – ні) та 12 мінорів першого порядку. Отже, для цієї матриці ранг r(A)=2.
має три мінори третього поряду (всі з яких дорівнюють нулю), дев’ять мінорів другого порядку (з яких деякі дорівнюють нулю, а деякі – ні) та 12 мінорів першого порядку. Отже, для цієї матриці ранг r(A)=2. у n-вимірному просторі. Ця система називається лінійно залежною, якщо існують такі числа k1,…km (не всі з яких одночасно дорівнюють нулю: k12+k22+…+km2>0), що
у n-вимірному просторі. Ця система називається лінійно залежною, якщо існують такі числа k1,…km (не всі з яких одночасно дорівнюють нулю: k12+k22+…+km2>0), що .
. є лінійно залежною, бо існують числа k1=1, k2=1/2, k3=1 такі, що k12+k22+…+km2 = 1+1/4+1 > 0 і одночасно
є лінійно залежною, бо існують числа k1=1, k2=1/2, k3=1 такі, що k12+k22+…+km2 = 1+1/4+1 > 0 і одночасно 
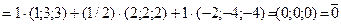 .
. та
та  є лінійно незалежною, бо рівність
є лінійно незалежною, бо рівність  , тобто
, тобто ,
,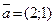 та
та  . Тоді для довільного вектора
. Тоді для довільного вектора  завжди знайдуться числа k1 та k2 такі, що
завжди знайдуться числа k1 та k2 такі, що 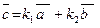 (рис. 1.2):
(рис. 1.2):


 y
y








 x
x . Тоді при k1=3 та k2= -1
. Тоді при k1=3 та k2= -1 .
. . Підсистема
. Підсистема  цієї системи називається базою (базисом), якщо
цієї системи називається базою (базисом), якщо є, наприклад, підсистема
є, наприклад, підсистема  .
. - квадратна матриця. Власними значеннями (власними числами, характеристичними числами) цієї матриці називаються такі значення параметра l , які задовольняють рівняння |A‑l×E| =0 , тобто рівняння
- квадратна матриця. Власними значеннями (власними числами, характеристичними числами) цієї матриці називаються такі значення параметра l , які задовольняють рівняння |A‑l×E| =0 , тобто рівняння (1.6)
(1.6) .
. .
. ;
; .
. .
. такий, що A×
такий, що A×  та
та 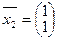 є власними векторами (що відповідають власним числам l1 =2 та l2 =3) матриці
є власними векторами (що відповідають власним числам l1 =2 та l2 =3) матриці  та
та  .
.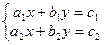 .
. , а розширену матрицю через
, а розширену матрицю через  .
. .
.

 .
.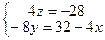 , знаходимо:
, знаходимо: .
. .
. .
. (i=1,…,n).
(i=1,…,n). . (1.7)
. (1.7) .
.

 ,
, .
. .
. .
. .
. ,
, .
. , тобто отримуємо систему рівнянь
, тобто отримуємо систему рівнянь , розв’язками якої є числа x1= -1; x2=2; x3=3.
, розв’язками якої є числа x1= -1; x2=2; x3=3.


 a11x1 a22x2
a11x1 a22x2
 a12x2
a12x2

 1 2 y2
1 2 y2 Промисловість с/г
Промисловість с/г


 a21x1
a21x1
 ЕОМ
ЕОМ
 .
.
 (1.8)
(1.8)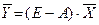 , (1.9)
, (1.9) . (1.10)
. (1.10)