 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 2. Аналітична геометрія
1. Вектори. 2. Аналітична геометрія на площині. 3. Аналітична геометрія в просторі.
2.1. Вектори
Означення. Вектором (n-вимірним вектором, геометричним вектором) називається впорядкований набір чисел Означення. Вектори називаються рівними, якщо співпадають їхні розмірності та всі компоненти. Приклад. Вектори (1;2;3) та (1;3;2) рівними не є, незважаючи на те, що множина {1;2;3} дорівнює множині {1;3;2} . Означення. Нульовим вектором називається вектор Означення. Добутком вектора Означення. Сумою векторів Означення. Скалярним добутком векторів Означення. Модулем (довжиною) вектора Кут j між векторами Вектори називаються ортогональними, якщо їхній скалярний добуток дорівнює нулю. Це виконується за умови cosj=0 , тобто при j=900. Розглянемо прямокутну систему координат на площині та вектори
Рис. 2.1.
Розглянемо також просторову систему координат з ортами
x Рис. 2.2.
Виконується така теорема: Кожен вектор в n-вимірному просторі єдиним способом розкладається по координатних осях. Зокрема, в тривимірному просторі
а в двовимірному
Нехай
Наведемо деякі формули, що стосуються векторів у тривимірному просторі. Кути між вектором
Кут між двома векторами
Означення. Векторним добутком векторів
Векторний добуток задовольняє, зокрема, таку властивість:
Приклад. Обчислити площу трикутника ABC, де A(1;0;2), B(1;2;0), C(0;1;2). Знаходимо вектори
Знаходимо модуль цього векторного добутку:
Отже, шукана площа
2.2. Аналітична геометрія на площині
Пряма лінія на площині найчастіше задається у вигляді рівняння y = k×x + b (2.3) де k=tga ‑ нахил цієї прямої до осі OX (рис 2.3,а). Часткові випадки розташування прямої (y=kx, x=a, y=b) показані, відповідно, на рис.2.3б-г.
a а б в г Рис.2.3
Загальне рівняння прямої на площині має вигляд Ax + By + C = 0 (2.2) Якщо B¹0 , то рівняння (2.2) можна перетворити у (2.1).
y=1-x 2
1 x -1 x а б Рис. 2.4 Наведемо ще деякі з рівнянь, які задають пряму на площині. Пряма, яка проходить через дві задані точки (x1;y1) та (x2;y2):
або, що те саме,
Пряма, яка проходить через задану точку (x1;y1) паралельно до заданої прямої y=ax+b : y-y1=a(x-x1) (2.4) Пряма, яка проходить через задану точку (x1;y1) перпендикулярно до заданої прямої y=ax+b :
Рівняння прямої у відрізках
Переходи від одного вигляду рівняння прямої до іншого виконують за допомогою нескладних перетворень. Приклад. Загальне рівняння прямої має вигляд 2x-y+2=0. Перейдемо до рівняння прямої у відрізках: -2x+y=2,
Перейдемо до рівняння з кутовим коефіцієнтом: y=2x+2. Візьмемо на нашій прямій дві точки, наприклад, (x1;y1)=(-1;0) та (x2;y2)=(0;2),і побудуємо рівняння прямої, яка проходить через ці дві точки:
Наведемо ще декілька формул щодо прямих на площині. Кут між прямими y=a1x+b1 та y=a2x+b2 обчислюється за формулою
Прямі y=a1x+b1 та y=a2x+b2 отже, є паралельними, якщо a1=a2, та перпендикулярними, якщо a1×a2 = -1. Точка перетину прямих є розв’язком системи рівнянь
Відстань від точки M(x1;y1) до прямої Ax+By+C=0 визначають за формулою
Приклад. Попит Q (кількість товару, що буде куплено) на товар залежно від його ціни p на ринку задається формулою p=p(Q)=500-10Q. Пропозицію Q (кількість товару, що потрапить на ринок) залежно від ціни задає формула p=p(Q)=50+5Q. Зобразити графічно криві попиту та пропозиції і визначити ціну рівноваги. Маємо такий графік (рис.2.5).
Попит
Q* Q Рис. 2.5.
Ціну рівноваги p* (а також рівноважний випуск Q*) визначаємо як точку перетину прямих попиту та пропозиції, тобто розв’язуємо систему лінійних рівнянь
Помноживши друге рівняння на 2 і додавши до першого, отримаємо p*=200 та Q*=30 . Приклад. Нехай ринкова ціна за одиницю деякого виробу становить p=10. Витрати, пов’язані з випуском кожної одиниці цього виробу в деякій фірмі, Vc=5 (змінні витрати). Постійні витрати фірми становлять Fc=40. Визначити обсяг виробництва Q, за якого фірма матиме прибуток. Загальні витрати фірми на виготовлення Q одиниць продукції описуються залежністю Tc = Fc + Q×Vc = 40+5Q . Доход фірми від виготовлення і реалізації Q одиниць продукції становить TR = p×Q =10Q . Визначимо такий випуск Q*, за якого доход фірми збігається з її витратами: TR = TC , 10Q = 40+5Q , Q* = 8 . Отже, прибуток (різниця між доходом і витратами) в цій моделі починається при Q*>8 і далі необмежено зростає (рис. 2.6).
TR(доход)=10Q
Tc(витрати)=40+5Q
Q*=8 Q Рис. 2.6.
Розглянемо також основні криві другого порядку та їхні рівняння. Це такі криві, рівняння яких містять змінні x2 і/або y2. Рівняння кола з центром у точці (a;b) та радіусом r має вигляд (x-a)2+(y-b)2=r2 . У частковому випадку (коло одиничного радіуса з центром у початку координат) це рівняння спрощується: x2+y2=r2 . Рівняння еліпса (геометричного місця точок, сума відстаней до яких від двох заданих точок є сталою) записується так (рис. 2.7):
c
F1 F2
Рис. 2.7.
Точки F1(-c;0) та F2(c;0) називаються при цьому фокусами. Виконуються такі властивості: - для довільної точки A на еліпсі - c2=a2-b2. Рівняння гіперболи (геометричного місця точок (x;y), для яких різниця відстаней до фокусів F1 та F2 є сталою) має вигляд (рис. 2.8):
Для гіперболи виконуються такі властивості: - для довільної точки A на гіперболі - c2=a2+b2.
y
F1(-c;0) F2(c;0)
Рис. 2.8.
Рівняння параболи (геометричного місця точок, однаково віддалених від заданої точки y = 2px
p/2 p/2
F
Рис. 2.9.
Тут для довільної точки A(x;y) параболи y = 2px виконується рівність
2.3. Аналітична геометрія в просторі
Загальне рівняння площини в тривимірному просторі, яка проходить через точку (x0;y0;z0) перпендикулярно до вектора A(x-x0)+B(y-y0)+C(z-z0) (2.7) або Ax+By+Cz=0 (2.8) Спеціальними площинами є площини OXY (рівняння z=0), OXZ (рівняння y=0) та OYZ (рівняння x=0). Рівняння площини, яка проходить через три задані точки (x0;y0;z0), (x1;y1;z1), (x2;y2;z2) (якщо ці точки не лежать на одній прямій), є таким:
Приклад. Записати рівняння площини, яка проходить через точки M0(1;2;3), M1(2;1;2) та M3(3;3;1). Маємо звідки x+4y-4=0. Рівняння площини у відрізках є таким:
Ця площина проходить через точки (a;0;0), (o;b;0) та (0;0;c). Приклад. Ціни за одиницю кожного з трьох товарів становлять, відповідно, 2, 3 та 4 умовні одиниці. Бюджет споживача дорівнює 120 умовних одиниць. Зобразити графічно бюджетне обмеження цього споживача. Нехай споживач на всі гроші купив x одиниць першого товару, y одиниць другого та z одиниць третього. Тоді виконується рівність 2x+3y+4z=120. Ми отримали бюджетне обмеження споживача як загальне рівняння площини. Зручніше записати це обмеження у вигляді рівняння площини у відрізках (виконавши ділення на 120):
`Отже, споживач може купити або тільки 60 одиниць першого товару, або тільки 40 другого, або тільки 30 третього, а також може перебувати в довільній іншій точці площин
частина площини в просторі
y x Рис. 2.10. Якщо ж витрачають не всі гроші, то бюджетне обмеження буде тетраедром:
Розглянемо випадок, коли споживач зовсім не купує третього товару (z =0). Тоді бюджетне обмеження представлятиме собою відрізок прямої на площині
або множину точок всередині трикутника (рис. 2.11)
y
Рис. 2.11. Рівняння прямої у тривимірному просторі також записується багатьма способами. Пряму як перетин двох площин задають системою лінійних рівнянь
Симетричне (канонічне) рівняння прямої, що проходить через точку (x0;y0;z0) паралельно до напрямного вектора
Параметричне рівняння прямої є таким:
Рівняння прямої в просторі, яка проходить через дві точки (x1;y1;z1) та (x2;y2;z2) , є подібним до рівняння прямої на площині:
Приклад. Пряма в просторі проходить через дві точки: M1(1;2;3) та M2(4;6;8) . Рівнянням цієї прямої згідно (2.14) є рівняння
Виконавши операції віднімання, отримуємо канонічне рівняння
Від останнього рівняння перейдемо до параметричного задання прямої (формула 2.13): У тривимірному просторі справджуються такі формули для кутів: кут між двома прямими обчислюється згідно з формулою кут між прямою
Тема 3. Послідовності
1. Послідовності та їхні границі. 2.Майбутня та теперішня вартість. 3.Використання техніки дисконтування в економічних задачах.
3.1. Послідовності та їхні границі
Означення. Послідовністю називається множина чисел {xn} = = x1,x2,…,xn,…, яка підпорядковується певному закону. Числова послідовість може бути як скінченною, так і нескінченною. Приклади послідовностей. 1. {xn} = 0, 1, 4, 9, 16, … Тут загальний член послідовності {xn} заданий формулою xn = n2. 2. 3. xn ‑ n-е за порядком просте число, тобто x1=1; x2=2; x3=3; x4=5; x5=7; x6=11;… Означення. Число A називається границею послідовності {xn}, якщо для довільного числа d>0 знайдеться такий номер N, починаючи з якого всі члени послідовності потрапляють у d-окіл числа A . Використовується запис За допомогою кванторів ∃ (“існує”) та ∀ (“для всіх”) останнє означення можна записати так:
Приклад. Розглянемо послідовність Для d=0,02 таким номером буде N=50 і так далі. Послідовність xn=n2 границі не має. Не має границі також послідовність 1,1; 2,1; 1,01;2,01;1,001;… Означення. Послідовність, яка має границю, називається збіжною. Послідовність, границею якої є число нуль, називається нескінченнно малою. Приклад. Нехай Наведена нижче теорема описує властивості границь послідовностей. Теорема. Якщо послідовності {xn} та {yn} збіжні, і
Якщо B¹0, то послідовність Приклади. 1. Знайти Це послідовність вигляду {xn×yn}. Згідно з теоремою
2. Знайти Маємо послідовність вигляду
Тепер 3. Знайти
Розглянемо дві числові послідовності спеціального вигляду. Приклад. Задано арифметичну прогресію: {an} = a1, a1+d, a2+d, a1+3d,… Величина d називається різницею прогресії. Загальний член an арифметичної прогресії обчислюють за формулою an=a1+(n-1)d. Сума перших членів прогресії Наприклад, для прогресії {xn} =2; 12; 32; 42; . . . an = 2+10(n-1) = 10n-8
Очевидно, що будь-яка арифметична прогресія є розбіжною послідовністю. Приклад. Задано геометричну прогресію b1; b1q; b1q2; b1q3; . . . Величина q називається знаменником геометричної прогресії. Загальний член прогресії має вигляд bn=b1qn-1. Сума перших членів прогресії Наприклад, для прогресії 1; 1/2; 1/4; 1/8;…;1/16;. . . загальний член bn=1×(1/2)n-1, а сума nперших членів ‑ При |q| < 1 послідовність b1; b1q; b1q2; b1q3; ... є нескінченно малою. Така послідовність називається нескінченою геометричною прогресією. Сума всіх членів нескінченної (нескінченно спадної) геометричної прогресії
Приклад. Сума всіх членів прогресії 1; 1/2; 1/4; 1/8; . . .
Приклад. Сума всіх членів прогресії 1; -1/2; 1/4; -1/8; . . .
3.2. Майбутня та теперішня вартість
Нехай p - початковий внесок в банк; r - процент (відсоток) нарахувань; t - кількість періодів, що минули від моменту початкового внеску. У тому випадку, коли нараховують звичайні відсотки, поточний розмір внеску є послідовністю типу арифметичної прогресії a0=p; a1=p+rp; a2=p+2rp; . . .; at=p+trp; . . . Загальний член прогресії (розмір внеску в періоді t ) обчислюють за формулою at=p(1+t×r).
Приклад. Клієнт вклав у банк 1000 грн. під прості відсотки у розмірі 10% річних. Визначити, через скільки періодів його внесок подвоїться. При p = 1000 грн. та r = 0,1=10% маємо a0=1000; a1=1100; a2=1200; . . . ; at=1000(1+0,1t); . . . Подвоєння внеску (at=2a0) відбудеться через 1/r=10 періодів (років). Справді, із рівняння 1000(1+0,1t) = 1000 ×2 отримуємо 1+0,1t = 2; t = 10.
Нехай, як і раніше, як і раніше, p - початковий внесок у банк; r - відсоток нарахувань; t - кількість періодів, що минули від моменту початкового внеску, проте в кінці кожного періоду нараховують відсотки не від початкового внеску, а від розміру останнього внеску (так звані складні відсотки). Тепер розміри внесків в кінці періодів будуть такими: b0 = p; b1 = p+rp =p(1+r); b2 = (p+rp)+r(p+rp) =p(1+r)2; . . . . . . . . . . . . . . . . . . . . . . . bt=p(1+r)t . . . . . . . . . . . . . . . . . . . . . Як бачимо, послідовність значень цих внесків є геометричною прогресією. При p=1000; r=0,1 (10%) у випадку складних відсотків розміри внесків будуть такими: b0=1000; b1=1000×1,1=1100; b2=1000×1,12=1210; . . . ;bt=1000×1,1t;. . . Подвоєння внеску ( bt=2b0 ) буде через 7,27 періоду (року). Справді, з рівняння 1,1t=2 маємо t×ln1,1=ln2, звідки Ми отримали результат: у разі нарахування складних відсотків у розмірі r через t періодів (місяців, років) внесок p зростає до p(1+r)t . Зокрема, кожна гривня зросте до (1+r)t гривень. Отже, майбутня вартість теперішніх грошей обчислюється за формулою
Позначення FV та PV представляють собою скорочення від слів Future Value (майбутня вартість) та Present Value (теперішня вартість). Очевидно, що теперішню вартість майбутніх грошейрозраховують за формулою
Обчислення теперішньої та майбатньої вартості виконують функції PV та FV (у російській версії використовуються не зовсім вдалі назви БЗ та ПЗ ) системи EXCEL . Приклад. Нараховують складні відсотки у розмірі 30%. Обчислити майбутню вартість (через два роки) теперішніх грошей у сумі 2000 грн. Згідно з формулою (3.3) маємо FV=2000(1+0,3)2=2000×1,69=3380 грн. Цей же результат дає застосування функції FV(0.3,2,0,-2000) або у російській версії БЗ(0,3;2;0;-2000).
3.3.Використання техніки дисконтування в економічних задачах
Обчислення за формулою (3.4) та аналогічними формулами називають дискотуванням. Техніка дисконтування дуже поширена у фінансових розрахунках. Наведемо кілька прикладів. Приклад. Банк приймає внески під складні відсотки у розмірі 6% (r=0,06) річних. Кожного року клієнт під ці відсотки кладе однакову суму грошей, не знімаючи їх. Якими повинні бути ці щорічні внески, щоб через три роки на рахунку стало 5000 грн.? Позначимо шукані шорічні внески через p. Спочатку на рахунку маємо S1 = p грн. Через один рік на цьому рахунку вже буде S2=[p+p(1+r)] грн. (новий внесок p та p(1+r), яка отримали з попереднього внеску). Через два роки ‑ S3 = p+p(1+r)+p(1+r)2 = p[1+(1+r)+(1+r)2] грн. І, нарешті, через t років матимемо загальний рахунок у розмірі St+1 = p[1+(1+r)+…+(1+r)t] грн. Зокрема, через три роки p[1+(1+r)+…+(1+r)3] = 5000 грн. Згідно з формулою (3.1)
Отже, Цей же результат отримуємо, використавши фінансову функцію ППЛАТ(0,06;3;0;-5000) системи EXCEL.
Приклад. Скільки грошей потрібно покласти під складні відсотки у розмірі r = 7%, щоби протягом чотирьох років знімати по 1200 грн. Після цих чотирьох років на рахунку не повинно бути нічого. Для того, щоб через один рік мати змогу зняти з рахунку 1200 грн., (тобто щоб мати майбутню вартість FV1=1200), потрібно сьогодні покласти на цей рахунок внесок (теперішню вартість PV1) у розмірі
Щоб мати змогу зняти з рахунку FV2=1200 грн. через два роки, потрібно сьогодні покласти на цей рахунок
Аналогічно, для забезпечення можливості знімання по 1200 грн. у кінці третього та четвертого років потрібно на початку мати на рахунку, відповідно,
Отже, всього потрібно вкласти
(тут використані формули (3.1) та (3.4)). Функція ПЗ(0,07;4;-1200;0) дає результат PV = 4064,65 грн. Приклад. Яким повинен бути теперішній внесок під 12% річних (складні відсотки), щоб мати змогу щороку (безконечно) знімати з рахунку по 1000 грн.? У нашому прикладі FV1 = FV2 = FV3 = … = FVn = …= 1000 грн. Кожну з цих майбутніх вартостей потрібно забезпечити відповідною теперішньою вартістю PV1, PV2, PV3, . . . , PVn, , . . Теперішній внесок PV, очевидно, повинен дорівнювати сумі всіх цих теперішніх вартостей. З використанням формули (3.4) отримуємо
Використавши тепер формулу (3.2) для суми нескінченно спадної геометричної прогресії, одержимо
Приклад (оцінка інвестиційного проекту). Нехай деякий проект потребує за перший рік вкладення 300 умовних одиниць інвестицій; за другий рік – теж 300 умовних одиниць і за третій – 200 умовних одиниць. Починаючи з третього року проект даватиме доход: 100 умовних одиниць за третій рік; 300 умовних одиниць – за четвертий; 400 – за п’ятий та 500 за шостий. Надалі доходу не буде. З’ясувати, чи вигідно вкладати інвестиції в цей проект (вважаючи, що ризику нема). Передбачено щорічну інфляцію у розмірі 20%. Задамо вхідні дані задачі такою таблицею:
Перерахуємо як інвестиції, так і доходи майбутніх років на теперішню вартість (тобто, звиконаємо дисконтування).
Отже, інвестувати цей проект невигідно.
Приклад (погашення кредитів). Нехай клієнтові надано кредит у розмірі K=50000 грн. на t= 10 років. Визначити розмір R щорічного внеску клієнта (вважають, що цей внесок повинен бути однаковим продовж усіх 10 років). Нараховують складні відсотки у розмірі r= 10% річних. Розглядаючи K як теперішню вартість, маємо
звідки Отже, клієнт упродовж 10 років повинен сплачувати по 8137,25 грн.
Поиск по сайту: |
 .
.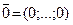 .
. .
. називається вектор
називається вектор  .
. .
.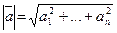 .
.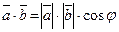 . При n=2 ця формула співпадає зі шкільною формулою для кута між векторами на площині.
. При n=2 ця формула співпадає зі шкільною формулою для кута між векторами на площині.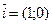 і
і  на цій площині (рис. 2.1). Ці вектори (вони ортогональні і їхня довжина дорівнює одиниці) називають ортами.
на цій площині (рис. 2.1). Ці вектори (вони ортогональні і їхня довжина дорівнює одиниці) називають ортами. y
y
 j
j i x
i x ,
,  та
та  (рис. 2.2).
(рис. 2.2). z
z


 k
k i j y
i j y ,
, .
. та
та  ‑ вектори, а k ‑ дійсне число. Виконуються такі властивості:
‑ вектори, а k ‑ дійсне число. Виконуються такі властивості: ;
; 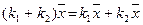 ;
; ;
;  ;
;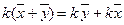 ;
;  ;
; ;
; 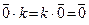 ;
;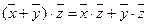 ;
;  .
. та координатними осями обчислюють за формулами
та координатними осями обчислюють за формулами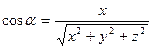 ;
; ;
;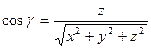 .
. та
та  обчислюєть за формулою
обчислюєть за формулою .
.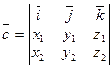
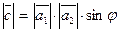 , де j ‑ кут між векторами
, де j ‑ кут між векторами  та
та  .
. =(0;2;-2) та
=(0;2;-2) та 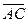 =(-1;1;0). Оскільки площа трикутника ABC дорівнює
=(-1;1;0). Оскільки площа трикутника ABC дорівнює  , то спочатку обчислюємо векторний добуток
, то спочатку обчислюємо векторний добуток .
.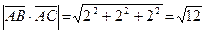
 .
.



 y y y y
y y y y

 b
b
 b
b




 Приклади. Побудувати графіки прямих y=1-x та 2x-y+2=0. У першому прикладі k=tga= -1, отже a=1350 (рис. 2.4,а). В другому прикладі маємо y=2x+2 , отже, k=tga=2 (рис. 2.4,б).
Приклади. Побудувати графіки прямих y=1-x та 2x-y+2=0. У першому прикладі k=tga= -1, отже a=1350 (рис. 2.4,а). В другому прикладі маємо y=2x+2 , отже, k=tga=2 (рис. 2.4,б). 2x-y+2=0
2x-y+2=0 a=1350
a=1350

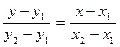 , (2.3)
, (2.3)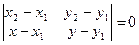 . (2.3¢)
. (2.3¢) (2.5)
(2.5) (2.6)
(2.6) .
.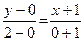 .
.
 .
. .
. p
p 500
500 Пропозиція
Пропозиція
 p*
p*
 .
.
 Tc,TR
Tc,TR
 40
40




 A(x;y)
A(x;y)
 ;
;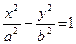
 ;
;

 A(x;y)
A(x;y)
 x
x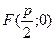 і заданої прямої
і заданої прямої 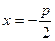 ) є таким (рис. 2.9):
) є таким (рис. 2.9):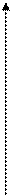



 B A(x;y)
B A(x;y)
 , де
, де  ‑ відстань від точки A до прямої
‑ відстань від точки A до прямої  .
. має вигляд
має вигляд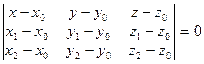 (2.9)
(2.9) ,
, . (2.10)
. (2.10) .
. за умов x³0; y³0; z³0 (рис .2.10).
за умов x³0; y³0; z³0 (рис .2.10). z
z Бюджетне обмеження –
Бюджетне обмеження –

 40
40 .
. ,
, .
.
 Бюджетне обмеження -
Бюджетне обмеження - 40 відрізок прямої на площині
40 відрізок прямої на площині 60 x
60 x . (2.11)
. (2.11) , має вигляд
, має вигляд . (2.12)
. (2.12) . (2.13)
. (2.13) . (2.14)
. (2.14) .
.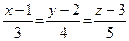 .
. .
.
 ;
; .
.
 .
. ≡ (∀d>0)(∃N)(∀n)[n>N ® |A-xn| < d]
≡ (∀d>0)(∃N)(∀n)[n>N ® |A-xn| < d] . Її границею є число 10. Зокрема, для d=0,1 номер N дорівнюватиме 10, оскільки
. Її границею є число 10. Зокрема, для d=0,1 номер N дорівнюватиме 10, оскільки  . Очевидно, що
. Очевидно, що 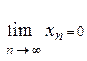 .., тобто xn ‑ нескінченно мала послідовність.
.., тобто xn ‑ нескінченно мала послідовність. , то послідовності {xn ± yn}, {xn × yn} також є збіжними, причому
, то послідовності {xn ± yn}, {xn × yn} також є збіжними, причому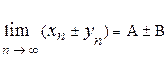 ,
,  .
. є збіжною, і
є збіжною, і  .
. .
. .
. .
. , у якій як послідовність {xn}={n+5} , так і послідовність {yn}={4n} не є збіжними. Для того, щоб застосувати попередню теорему, потрібно спершу виконати штучний прийом: поділити як чисельник, так і знаменник на n .
, у якій як послідовність {xn}={n+5} , так і послідовність {yn}={4n} не є збіжними. Для того, щоб застосувати попередню теорему, потрібно спершу виконати штучний прийом: поділити як чисельник, так і знаменник на n . .
. .
.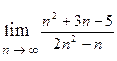
 .
. .
.
 . (3.1)
. (3.1) , зокрема, S2=3/2.
, зокрема, S2=3/2. (3.2)
(3.2) .
. (тут q = - 1/2 ).
(тут q = - 1/2 ). і t=7,27.
і t=7,27. (3.3)
(3.3) (3.4)
(3.4) ,
, грн.
грн. грн.
грн. грн.
грн. та
та  грн.
грн.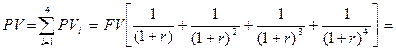


 грн.
грн. (у.о),
(у.о), (у.о).
(у.о).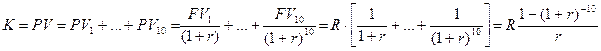 ,
, грн.
грн.