 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Первый замечательный предел. Следствия из первого замечательного предела
Второй замечательный предел. Следствия из второго замечательного предела.
Первый замечательный предел. Следствия из первого замечательного предела Первый замечательный предел имеет вид
и он позволяет раскрывать неопределенность Наряду с формулой (1) можно также непосредственно доказать следующие формулы (следствия из первого замечательного предела)
На практике же при решении примеров применяются не формула (1) и ее следствия (2), а следующие формулы
или цепочка эквивалентностей
Пример 1. Вычислить пределы (раскрыть неопределенность 1) Решение. 1) Для решения предела воспользуемся цепочкой эквивалентности:
В результате получим 2) В пределе
(воспользовались формулой разности косинусов
В результате получим 3) Упростим числитель и знаменатель (выделим синусы), чтобы привести к цепочке эквивалентностей:
Тогда применяя цепочку эквивалентностей, получим
Пример 2. Вычислить пределы (раскрыть неопределенность 1) Решение. 1) Для решения воспользуемся преобразованиями
Чтобы применить первый замечательный предел, сделаем линейную замену переменной:
2) Сделаем замену переменной
3) Учитываем, что
(использовали цепочку эквивалентностей
Второй замечательный предел. Следствия из второго Замечательного предела. В более подробном курсе математического анализа доказывается, что функция
На практике при решении примеров используется следующая формула
Формула (2) применяется для вычисления пределов вида Пример 1. Вычислить пределы: 1) Решение 1) Первоначально оцениваем предел
После выделения числа
2) Имеем
Пример 2. Вычислить предел Решение. В пределе примем
Вычисляем отдельно предел
Докажем далее следующие вспомогательные пределы (
Для доказательства формулы (3) достаточно подогнать предел под формулу (2) (используя свойство логарифма
Для доказательства формулы (4) сначала сделаем замену переменной
На основании формул (2), (4) докажем формулы (
Выделим в числителе
а затем применим формулу (4)
Пример 3. Вычислить предел Решение. В пределе сделаем замену
Пример 4. Вычислить предел Решение. Вынесем в числителе
Используя далее цепочки эквивалентностей
Пример 5. Вычислить предел Решение. В пределе делаем замену переменной
Для вычисления последнего предела воспользуемся методом сопряженных выражений:
Лекция 6
Поиск по сайту: |
 (1)
(1) , причем в пределе присутствуют тригонометрические функции.
, причем в пределе присутствуют тригонометрические функции.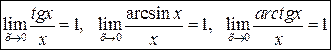 . (2)
. (2) ,
,  ,
,  ,
,  (3)
(3) при
при  . (4)
. (4) ; 2)
; 2)  ; 3)
; 3)  .
.  , так как
, так как  при
при 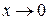 ,
, , так как
, так как 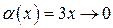 при
при  .
. , чтобы воспользоваться цепочкой эквивалентности
, чтобы воспользоваться цепочкой эквивалентности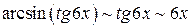 , так как
, так как  при
при 
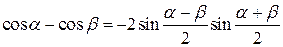 ).
). .
. ,
, .
.
 .
. ; 2)
; 2)  ; 3)
; 3)  .
. 

 , при этом
, при этом 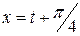 . Если
. Если  , то
, то  . Тогда получим
. Тогда получим
 .
. . При этом
. При этом  и если
и если  , то
, то  . Тогда
. Тогда


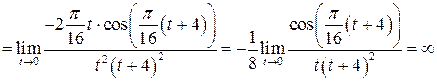 .
. . Сделав линейную замену переменной
. Сделав линейную замену переменной  (
(  и
и 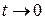 при
при  ), получим
), получим

 ,
,  при
при  имеет пределом число
имеет пределом число  , то есть
, то есть . (1)
. (1) . (2)
. (2) (их называют “пределами типа
(их называют “пределами типа  ”), причем
”), причем  ,
,  (то есть раскрытие степенно-показательной неопределенности
(то есть раскрытие степенно-показательной неопределенности  ). Покажем на примерах применение формулы (2).
). Покажем на примерах применение формулы (2). ; 2)
; 2) 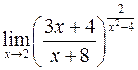 .
.  и получаем неопределенность
и получаем неопределенность  (
(  ) и затем “подогнать” предел под формулу (2). В нашем примере приравняем дробь
) и затем “подогнать” предел под формулу (2). В нашем примере приравняем дробь 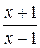 к выражению
к выражению  :
:  . Тогда отсюда
. Тогда отсюда  , причем
, причем  . Применяя формулу (2), получим
. Применяя формулу (2), получим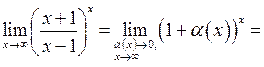
 .
. , учитывая, что
, учитывая, что  :
:
 .
.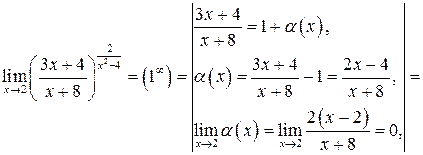


 .
. .
.  ,
,  . Последовательно подгоняя предел под формулу (8.2), получаем
. Последовательно подгоняя предел под формулу (8.2), получаем



 .
.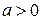 ,
,  )
) ,
,  , (3)
, (3) ,
,  . (4)
. (4)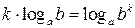 ,
,  ):
): .
. . При этом
. При этом  ,
,  , причем при
, причем при  . Теперь подгоняем под формулу (2)
. Теперь подгоняем под формулу (2) На практике при решении примеров удобнее пользоваться следующими эквивалентностями (следствиями из формул (3), (4))
На практике при решении примеров удобнее пользоваться следующими эквивалентностями (следствиями из формул (3), (4)) при
при 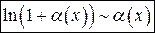 при
при  при
при  при
при  )
) , (9)
, (9) при
при  число
число 
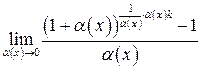
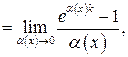
 .
. .
.  , при этом
, при этом  ,
,  . Используя эквивалентности (6), (8), получим
. Используя эквивалентности (6), (8), получим


 .
.  за скобки (
за скобки (  ), а в знаменателе воспользуемся формулой разности синусов. Тогда получим
), а в знаменателе воспользуемся формулой разности синусов. Тогда получим .
. ,
, , при
, при  .
. .
. 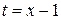 (
(  ,
, 
 .
. .
.