 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПРОВЕРКА ГИПОТЕЗЫ О ВИДЕ РАСПРЕДЕЛЕНИЯ ⇐ ПредыдущаяСтр 5 из 5
Проверка гипотезы о законе распределения значения признака X в генеральной совокупности осуществляется с помощью критериев согласия. Проверяемая (нулевая) гипотеза утверждает, что значения признака в выборка, взятой из генеральной совокупности, распределены по предполагаемому закону. Для проверки гипотезы о виде распределения необходимо вычислить теоретически ожидаемые (выравнивающие) частоты, которые должны были бы получиться, если бы распределение действительно соответствовало предполагаемому. Теоретические частоты 1) в случае дискретной СВ 2) в случае непрерывной случайной величины В частности для нормального закона распределения теоретические частоты рассчитываются по формуле:
где Проверку гипотезы о виде теоретического распределения можно провести с помощью критерия согласия Пирсона
где Гипотеза отвергается, если вычисленное значение Например, если проверяется согласие экспериментальных данных нормальному закону распределения, для которого r =2, то число степеней свободы Следует учитывать, что при использовании критерия согласия Пирсона общее число наблюдений должно быть достаточно большим ( Проверим для нашего примера гипотезу о нормальном законе распределения изучаемой величины для уровня значимости Найдём выравнивающие частоты. Таблица 3
Находим
Определим
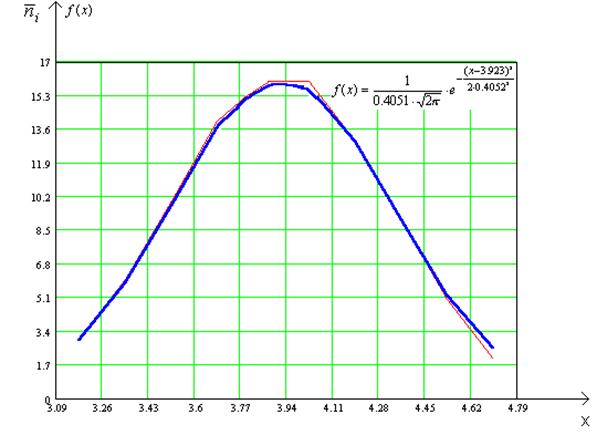
7.291<11.1. Следовательно, в рассматриваемом примере нет оснований отвергнуть гипотезу о нормальном распределении изучаемой случайной величины. Вид функции плотности вероятности исследуемой случайной величины, распределённой по нормальному закону, в нашем случае:
Функция распределения:
Приложение 1 Таблица значений функции
Приложение 2
Критические точки распределения χ2
ЛИтература
1. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для студентов вузов. М.: «Высшая школа», 2002. 2. Гмурман.В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: «Высшая школа», 2002. 3. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. – М..: Высшая школа, 1982. – Ч. 1 и 2.
СОДЕРЖАНИЕ
Введение........................................................................................... 5 1. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 7 2. ПОСТРОЕНИЕ ВАРИАЦИОННОГО РЯДА................................... 8 3. ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ВАРИАЦИОННЫХ РЯДОВ.. 9 4. ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ (КУМУЛЯТА) 11 5. ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ................... 13 6. ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ ОЦЕНКИ ПАРАМЕТРОВ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ……………………………………18 7. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ.............................. 22 8. ПРЕДВАРИТЕЛЬНЫЙ ВЫБОР ЗАКОНА РАСПРЕДЕЛЕНИЯ……24
9. ПРОВЕРКА ГИПОТЕЗЫ О ВИДЕ РАСПРЕДЕЛЕНИЯ.............. 25 Приложение 1...................................................................................... 31 Приложение 2...................................................................................... 32 ЛИтература..................................................................................... 33
Ирина Михайловна Баранова Наталья Александровна Часова Галина Дмитриевна Алексеева Анатолий Николаевич Муравьев
Методические указания к выполнению РГР для студентов очного и заочного обучения «Статистическая обработка большой выборки»
Лицензия НД №14185 от 6.03.2001 г. Формат 60 Брянская государственная инженерно-технологическая академия. 241037, г. Брянск, пр. Станке Димитрова, 3, редакционно–издательский отдел. Подразделение оперативной печати. Подписано к печати _____ мая 2006 г.
Поиск по сайту: |
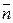 вычисляются по формулам:
вычисляются по формулам: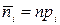 , где
, где 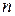 - объем выборки;
- объем выборки; 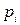 - вероятность случайной величины принять значение, равное
- вероятность случайной величины принять значение, равное  .
.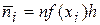 , где
, где 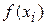 - функция плотности теоретического распределения, вычисленная в точке
- функция плотности теоретического распределения, вычисленная в точке 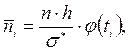
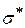 – среднее квадратическое отклонение,
– среднее квадратическое отклонение,  – табулированная функция,
– табулированная функция,  .
.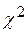 , основанного на статистике:
, основанного на статистике:
 – опытные частоты,
– опытные частоты, 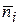 – выравнивающие частоты.
– выравнивающие частоты.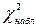 окажется больше критического
окажется больше критического 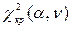 , найденного по таблицам распределения
, найденного по таблицам распределения 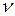 = l–r–1 где l –число интервалов, r – число оцениваемых параметров предполагаемого теоретического распределения (приложение 2).
= l–r–1 где l –число интервалов, r – число оцениваемых параметров предполагаемого теоретического распределения (приложение 2). 50), и число наблюдений в интервалах должно быть не менее пяти (
50), и число наблюдений в интервалах должно быть не менее пяти (  5). Интервалы, у которых
5). Интервалы, у которых 
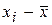
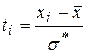
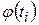

 5
5
 3
3
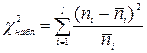 :
: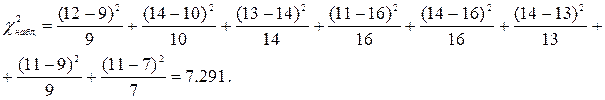
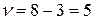 , уровень значимости
, уровень значимости  . Следовательно,
. Следовательно,  .
.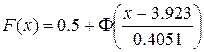 .
.
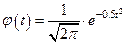
 94 1/16. Тираж 50 экз. Печ. л. – 2,0
94 1/16. Тираж 50 экз. Печ. л. – 2,0