 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПРЕДВАРИТЕЛЬНЫЙ ВЫБОР ЗАКОНА РАСПРЕДЕЛЕНИЯ
Большинство применяемых в практике контроля статистических методов основано на предположении, что распределение контролируемого признака подчиняется определенному теоретическому закону (нормальному, биноминальному, пуассоновскому и так далее) с параметрами, либо оцениваемыми по выборке, либо заранее известными. Применению этих методов должна предшествовать проверка по данным выборочных наблюдений гипотезы о законе распределения. Чаще всего на практике имеют дело с нормальным распределением. Чем это объясняется? Ответ на этот вопрос дан А.М.Ляпуновым в центральной предельной теореме теории вероятности. Приведем следствие из нее: если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному. Функция плотности нормального закона распределения имеет вид У нормального распределения два параметра (r =2): математическое ожидание Кривая нормального распределения симметрична относительно прямой
1) Для нормального закона средняя арифметическая
У нас: 2) У кривой нормального распределения коэффициенты асимметрии и эксцесса равны нулю. У нас: 3) В случае нормального распределения справедливо следующее условие:
Проверим выполнение этого условия для нашего примера. В нашем случае выборочные коэффициенты асимметрии и эксцесса равны 4) На практике для выдвижения гипотезы о нормальном распределении используют правило 3-х сигм: если случайная величина распределена нормально, то абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднеквадратического отклонения, т.е. все значения случайной величины должны попасть в интервал: В нашем случае все значения величины попадают в интервал
Рисунок 5 - Правило 3-х сигм.
Таким образом, у нас есть основания предположить, что изучаемая случайная величина распределена по нормальному закону (нулевая гипотеза)
Поиск по сайту: |
 , а интегральная функция распределения -
, а интегральная функция распределения - 
 и среднее квадратическое отклонение
и среднее квадратическое отклонение  . Их оцениваем по выборке:
. Их оцениваем по выборке: 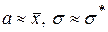 .
. .
.
 , мода
, мода  и медиана
и медиана  равноправны, как характеристики центра распределения:
равноправны, как характеристики центра распределения:
 . Как видно, значения этих величин отличаются друг от друга. Это можно объяснить тем, что три интервала имеют одинаковую частоту, которая является максимальной.
. Как видно, значения этих величин отличаются друг от друга. Это можно объяснить тем, что три интервала имеют одинаковую частоту, которая является максимальной. . Как видно, значение коэффициента асимметрии можно считать равным нулю, тогда как значение коэффициента эксцесса значительно отличается от нуля. Это можно объяснить неоднородностью статистического материала.
. Как видно, значение коэффициента асимметрии можно считать равным нулю, тогда как значение коэффициента эксцесса значительно отличается от нуля. Это можно объяснить неоднородностью статистического материала. .
. , следовательно, условие выполнено, а именно для
, следовательно, условие выполнено, а именно для  :
:  ,
, 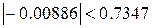 ; для
; для 
 ,
, 
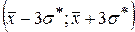 .
. , т.к.
, т.к. 


 .
.