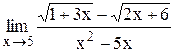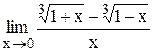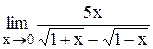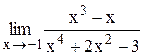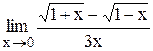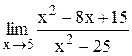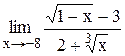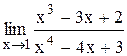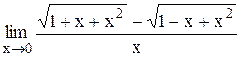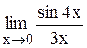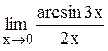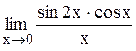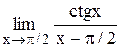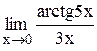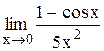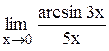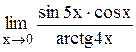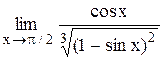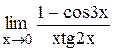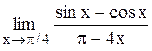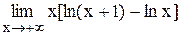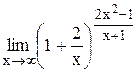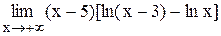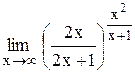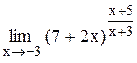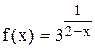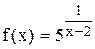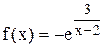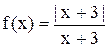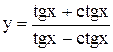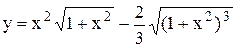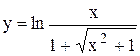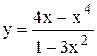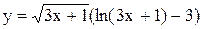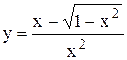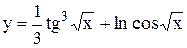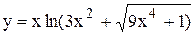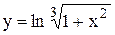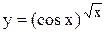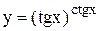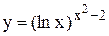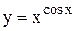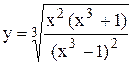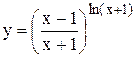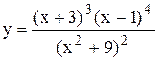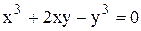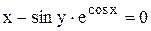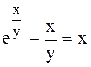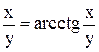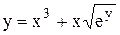|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Производная функции, заданной параметрически ⇐ ПредыдущаяСтр 3 из 3
Пусть функция
Пример 5. Найти Решение.
Логарифмическое дифференцирование
Если дана сложная функция, представляющая собой произведение или частное нескольких функций, причем числитель и знаменатель дроби в свою очередь содержат произведения, то следует обе части данного выражения сначала прологарифмировать по основанию у, применить соответствующие свойства логарифмов, а затем приступить к дифференцированию обеих частей. Этот прием носит название логарифмического дифференцирования. Его также используют, если функция содержит корни из дробей. К этому приему прибегают, если имеется показательно-степенная функция или функция вида Пример 6. Найти производную функции Решение. Логарифмируем обе части равенства по основанию е
Применяя свойства логарифмов, получаем
Дифференцируем обе части, считая y сложной функцией переменной х:
Пример 7.Найти производную функции Решение. Логарифмируем обе части по основанию е
Используя свойство логарифма, получаем,
Дифференцируем обе части, считая y сложной функцией переменной х
Замечание. При дифференцировании степенно-показательной функции можно пользоваться формулой
если f(x) и j(х) - дифференцируемые функции.
Индивидуальные задания Задание 1 Вычислить предел функции, числовой последовательности, раскрыв неопределенность типа Таблица 2
Продолжение табл.2
Задание 2 Вычислить предел функции, раскрыв неопределенность типа Таблица 3
Продолжение табл.3
Задание 3 Вычислить предел функции, используя I замечательный предел и его вариации. Задания взять из таблицы 4. Таблица 4
Продолжение табл.4
Задание 4 Вычислить предел функции, используя II замечательный предел. Задания взять из таблицы 5. Таблица 5
Продолжение табл.5
Задание 5 Исследовать функцию на непрерывность и построить график функции. Задания взять из таблицы 6. Таблица 6
Продолжение табл.6
Продолжение табл.6
Задание 6 Найти производную функции. Задания взять из таблицы 7. Таблица 7
Продолжение табл.7
Задание 7 Найти производную функции. Задания взять из таблицы 8. Таблица 8
Продолжение табл.8
Задание 8 Используя логарифмическое дифференцирование, найти производную функции. Задания взять из таблицы 9. Таблица 9
Продолжение табл.9
Задание 9 Найти производную неявно заданной функции. Задания взять из таблицы 10. Таблица 10
Продолжение табл.10
©2015-2020 studopedya.ru Все права принадлежат авторам размещенных материалов.
|
 определена параметрически:
определена параметрически:  ,
,  . Тогда, если функции x(t) и y(t) имеют производные в точке
. Тогда, если функции x(t) и y(t) имеют производные в точке  , причем
, причем  , а функция
, а функция  имеет производную в точке
имеет производную в точке  , то эта производная находится по формуле
, то эта производная находится по формуле или
или 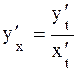 .
. для заданной параметрически функции
для заданной параметрически функции  .
.
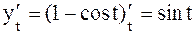
 .
. .
. .
. .
. .
.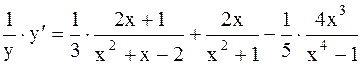
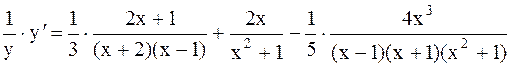
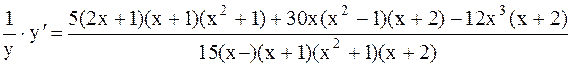
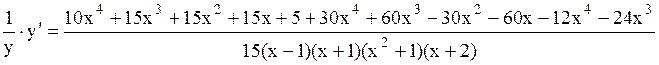
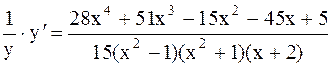
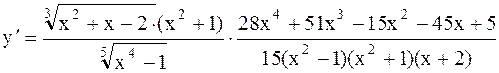
 .
. .
. .
. .
.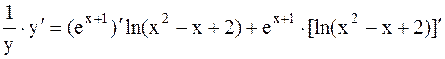
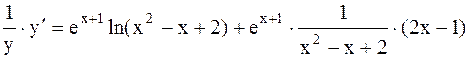
 .
.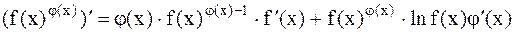 ,
, . Задания взять из таблицы 2.
. Задания взять из таблицы 2.

















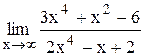

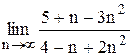




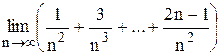



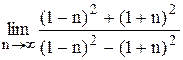




















 . Задания взять из таблицы 3
. Задания взять из таблицы 3