 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Предел числовой последовательности и функцииСтр 1 из 3Следующая ⇒
Пределы числовой последовательности и функции. Непрерывность функции. Дифференцирование функции Модуль-1 (МА)
Курск 2005 Составитель: З.Г.Гончарова УДК 517
Рецензент Кандидат технических наук, доцент кафедры высшей математики Н.А. Моргунова
Пределы числовой последовательности и функции. Непрерывность функции. Дифференцирование функции[Текст]: методические указания и индивидуальные задания. Модуль-1 по математическому анализу / сост.: З.Г.Гончарова; Курск. гос. техн. ун-т; Курск, 2005. 41 с., табл. 11. Библиогр.: 5 назв.
Излагаются краткие методические рекомендации по темам математического анализа: пределы числовой последовательности и функции, непрерывность функции, дифференцирование функции. В работе представлены 50 вариантов индивидуальных заданий.
Методические указания и индивидуальные задания предназначены для студентов технических специальностей.
.
Текст печатается в авторской редакции
ИД №06430 от 10. 12. 2001. Подписано в печать ________ . Формат 60х84 1/16. Печать офсетная. Усл. печ. л. Уч.-изд. л. .Тираж 50 экз. Заказ ……. Бесплатно. Курский государственный технический университет. Издательско-полиграфический центр Курского государственного технического университета. 305040 Курск, ул. 50 лет Октября, 94. Содержание
Введение………………………………………………………………4 1. Предел числовой последовательности и функции………………5 2. Сравнение бесконечно малых функций………………………...10 3. Непрерывность функции………………………………………...11 4. Дифференцирование функции…………………………………..14 4.1. Производная сложной функции…………………………….14 4.2. Производная функции, заданной в неявном виде…………15 4.3. Производная функции, заданной параметрически………...16 4.4. Логарифмическое дифференцирование……………………17 5. Индивидуальные задания………………………………………...19 Контрольные вопросы…………………………….………………...40 Список рекомендуемой литературы……………………………….41
Введение Основной формой обучения студентов является самостоятельная работа с учебником и учебными пособиями. Поэтому каждый студент с самого начала занятий должен выработать для себя рациональную систему работы над курсом, постоянно практикуясь при этом в решении задач. В противном случае усвоение и практическое использование материала затруднены. Чрезвычайно важны систематические занятия. Работа урывками не приносит положительных результатов. Часто приходится слышать высказывания студентов о том, что теорию они знают, а решать задачи не умеют. Данная работа содержит методические указания по выполнению модуля системы РИТМо, который способствует развитию индивидуального творческого мышления, обеспечивает ритмическую работу студента при изучении разделов математического анализа: пределы числовой последовательности и функции, дифференцирование функции, исследование функции на непрерывность. Каждый параграф начинается с краткого теоретического введения, приводятся основные определения, методы и способы решения задач. Рассмотрение решения типовых примеров и задач в параграфе, как правило, расположено по возрастающей трудности. Здесь же представлены индивидуальные задания, которые даны в объеме 50 вариантов. Номер варианта дает лектор. Он приводит общую нумерацию студентов в потоке. Для подготовки к защите модуля представлен список контрольных вопросов. Для выполнения модуля достаточно аккуратно записанных лекций и внимательного изучения методических рекомендаций, предложенных в данном учебном пособии. Кроме того, весь теоретический материал по данным темам хорошо представлен в учебных пособиях, указанных в списке литературы.
Предел числовой последовательности и функции
Определение 1. Число А называется пределом функции f(x) в точке a, если для любого e>0 найдётся такое число d>0, что из неравенства Определение 2. Число А называется правым (левым) пределом функции f(х) в точке а, если для любого Для обозначения правого (левого) предела функции f(x) в точке а используют следующую символику: Критерий существования предела. Для того, чтобы в точке
Достаточно распространенными в курсе математики являются последовательности, то есть функции Определение 3. Число В называется пределом последовательности f(n), если для произвольного При вычислении пределов обычно используют не определение предела, а теоремы о пределах и приёмы, которые мы обобщим, оформив результат в форме табл. 1.
Таблица 1 Практическое вычисление пределов
Продолжение табл.1
При нахождении пределов вида 1) если существуют конечные пределы 2) если 3) если Пример 1. Найти Решение. Здесь следовательно, Пример 2. Найти Решение. Имеем Поэтому Пример 3. Найти Решение. Здесь
Можно найти предел проще, не прибегая к общему приёму, а именно
Поиск по сайту: |
 следует неравенство
следует неравенство  .
. найдётся такое число
найдётся такое число  , что из неравенства
, что из неравенства 
 следует неравенство
следует неравенство  .
.
 .
. существовал предел функции f(x), необходимо и достаточно, чтобы существовали и были равны между собой оба односторонних предела
существовал предел функции f(x), необходимо и достаточно, чтобы существовали и были равны между собой оба односторонних предела .
. , заданные на множестве натуральных чисел N. Чтобы подчеркнуть, что аргумент такой функции принимает только значения из множества натуральных чисел, его обозначают не х, а n. Для последовательностей f(n) достаточно часто возникает необходимость найти ее предел при неограниченном возрастании аргумента n (при
, заданные на множестве натуральных чисел N. Чтобы подчеркнуть, что аргумент такой функции принимает только значения из множества натуральных чисел, его обозначают не х, а n. Для последовательностей f(n) достаточно часто возникает необходимость найти ее предел при неограниченном возрастании аргумента n (при  ).
). существует такое число
существует такое число  , что для всех
, что для всех 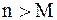 выполняется неравенство
выполняется неравенство  .
.

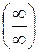 , то пробуем в числителе и знаменателе вынести за скобки переменную в наивысшей степени (или числитель и знаменатель делим на переменную в наивысшей степени)
, то пробуем в числителе и знаменателе вынести за скобки переменную в наивысшей степени (или числитель и знаменатель делим на переменную в наивысшей степени)



 , то:
, то:
 =
= 
 2 способ
Обозначим
2 способ
Обозначим  . Тогда
. Тогда  . При x®4, t®2.
Тогда
. При x®4, t®2.
Тогда 
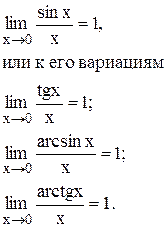
 Сократив числитель и знаменатель на переменные, которые стоят за скобками, учитывая, что
Сократив числитель и знаменатель на переменные, которые стоят за скобками, учитывая, что  , и учитывая первый замечательный предел и его вариации, получаем, что искомый предел равен:
, и учитывая первый замечательный предел и его вариации, получаем, что искомый предел равен:

 следует иметь в виду, что:
следует иметь в виду, что: и
и 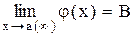 , то
, то 
 и
и 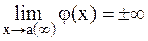 , то вопрос о нахождении предела С решается непосредственно;
, то вопрос о нахождении предела С решается непосредственно; , то есть имеем неопределённость вида
, то есть имеем неопределённость вида  , то используем 2-ой замечательный предел
, то используем 2-ой замечательный предел  или
или 

 ,
, .
. .
.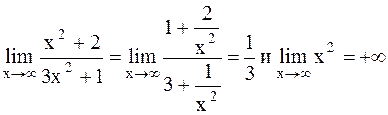
 .
. .
. то есть имеем неопределённость вида
то есть имеем неопределённость вида 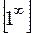 . В этом случае, прежде чем применить 2-ой замечательный предел, произведём следующие преобразования:
. В этом случае, прежде чем применить 2-ой замечательный предел, произведём следующие преобразования:
 Замечание. Если существует и положителен
Замечание. Если существует и положителен  то
то 