 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Cравнение бесконечно малых функций
Определение. Если Пусть функции a(х) и b(х) являются бесконечно малыми при х®х 1) если 2) если 3) если a(х)~b(х). Аналогичные определения можно сформулировать и при х®+¥, х®-¥, х®¥, х®х При вычислении пределов пользуются следующей теоремой: предел произведения или частного бесконечно малых функций не изменится, если любую из них заменить эквивалентной ей бесконечно малой функцией. Пусть a(х) - бесконечно малая функция при х®х 1) sina(х)~a(х); 2) tga(х)~a(х); 3) arcsina(x)~a(x); 4) arctga(x)~a(x); 5) log(1+a(x))~ 7) a 9) (1+a(x)) Пример 1. Найти Решение. Так как sin x ~ x, a arctg 2x ~ 2x при х®0, то
Пример 2. Найти Решение. Здесь
Непрерывность функции
Функция f(x) называется непрерывной в точке а, если: 1) эта функция определена в некоторой окрестности точки а; 2) существует предел 3) этот предел равен значению функции в точке а, т.е. Если функция непрерывна в каждой точке некоторой области, то она называется непрерывной в этой области. Те точки области определения функции, в которых функция не является непрерывной, называются точками разрыва функции. Различают разрывы двух видов. 1. Если в точке а существуют односторонние пределы функции, но, по крайней мере, один из них не равен значению данной функции в точке а, то говорят, что функция f(x) в точке а имеет разрыв первого рода. При этом возможны следующие случаи: f(a-0)=f(a+0)¹f(a) (в этом случае говорят, что функция f(x) в точке а имеет устранимый разрыв); f(a-0)¹f(a+0) (в этом случае говорят, что функция f(x) в точке а имеет разрыв с конечным скачком. При этом число ïf(a+0) - f(a-0)ïназывают скачком функции f(x) точке а). 2. Функция f(x) в точке а имеет разрыв второго рода, если в этой точке по крайней мере, один из односторонних пределов бесконечен или вовсе не существует. Функция f(x) называется непрерывной на отрезке Непрерывные на отрезке функции обладают рядом важных свойств. Приведём одно из них. Пусть функция f(х) непрерывна на отрезке В задачах 1-5 определить, какого рода разрывы имеют следующие функции в точке а
Пример 1. Решение. Если х®3-0, то Пример 2. Решение. Выделим целую часть Таким образом, функция при х®1 не имеет ни левого, ни правого конечного предела. Следовательно, х=1 является точкой разрыва 2-го рода. Пример 3. Решение. Если Пример 4. Решение.
Пример 5. Решение. Если х®1-0, то
Поиск по сайту: |

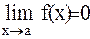 , то f(x) называется бесконечно малой при x®a.
, то f(x) называется бесконечно малой при x®a. . Тогда:
. Тогда: , то a(х) называется бесконечно малой функцией более высокого порядка, чем b(х) при х®х
, то a(х) называется бесконечно малой функцией более высокого порядка, чем b(х) при х®х 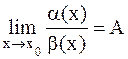 , где А -конечное число, отличное от нуля, то a(х) и b(х) называются бесконечно малыми функциями одного порядка при х®х
, где А -конечное число, отличное от нуля, то a(х) и b(х) называются бесконечно малыми функциями одного порядка при х®х 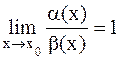 , то a(х) и b(х) называются эквивалентными бесконечно малыми функциями при х®х
, то a(х) и b(х) называются эквивалентными бесконечно малыми функциями при х®х  ;
;  ~a(x)lna; 8) e
~a(x)lna; 8) e  ~аa(х).
~аa(х).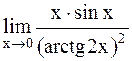 .
.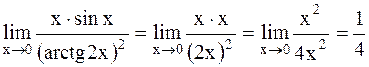 .
.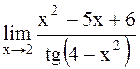 .
.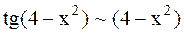 при х®2, поэтому
при х®2, поэтому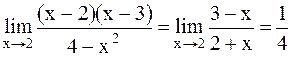 .
.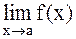 ;
;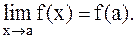
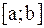 , если она непрерывна в каждой точке этого отрезка, причём в точке а она непрерывна справа (f(a+0)=f(a)), а в точке в - слева (f(b-0)=f(b)).
, если она непрерывна в каждой точке этого отрезка, причём в точке а она непрерывна справа (f(a+0)=f(a)), а в точке в - слева (f(b-0)=f(b)). существует такая точка c, в которой данная функция равна нулю.
существует такая точка c, в которой данная функция равна нулю.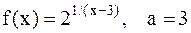
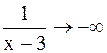 и
и  . Если х®3+0, то
. Если х®3+0, то 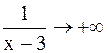 и
и 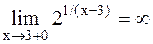 . Так как один из односторонних пределов бесконечен, следовательно, а=3-точка разрыва 2-го рода.
. Так как один из односторонних пределов бесконечен, следовательно, а=3-точка разрыва 2-го рода.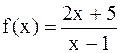 , а=1.
, а=1. . Если
. Если  , то
, то  и
и 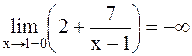 . Если х®1+0, то
. Если х®1+0, то  и
и  .
.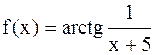 , а = -5.
, а = -5.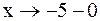 , то
, то 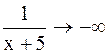 и
и 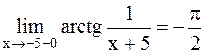 . Если
. Если 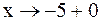 , то
, то  и
и 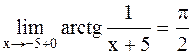 . Итак, при х® -5 функция имеет левый и правый конечные пределы, причём эти пределы различны. Следовательно, х = -5 является точкой разрыва 1-го рода. Разность между правым и левым пределами (скачок) в точке разрыва равна
. Итак, при х® -5 функция имеет левый и правый конечные пределы, причём эти пределы различны. Следовательно, х = -5 является точкой разрыва 1-го рода. Разность между правым и левым пределами (скачок) в точке разрыва равна 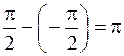 .
.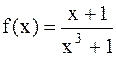 , а = -1.
, а = -1.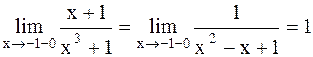 ,
, . Итак,
. Итак,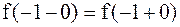 , но не равны
, но не равны  , значит, а=1 является устранимой точкой разрыва.
, значит, а=1 является устранимой точкой разрыва.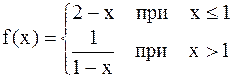 ,
, 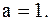
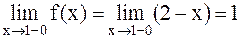 . Если х®1+0, то
. Если х®1+0, то 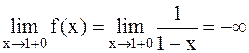 . Один из односторонних пределов бесконечен, следовательно,
. Один из односторонних пределов бесконечен, следовательно, 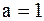 -точка разрыва 2-го рода.
-точка разрыва 2-го рода.