 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Отношение многочленов. Иррациональность
Исследуем поведение многочлена
становится очевидным (теоремы о пределе суммы и произведения), что Пример 1. Как ведут себя многочлены Решение. 1) т.к. выражение в скобках стремится к 2>0, а множитель 2) здесь знак результата определяет множитель 3) т.к. выражение в скобках стремится к -5<0, а множитель 4) здесь знак результата в силу чётности множителя
Таким образом, при стремлении аргумента
Пример 2. Найти а) Решение. а) Вынесем за скобки и в числителе, и в знаменателе старшую степень
После сокращения на
б) Вынесем за скобки старшую степень числителя
Теперь и числитель, и знаменатель при
При наличии иррациональности неопределённость Пример 3.Найти предел функции Решение. Данная функция при
Пример 4.Найти Решение. В числителе старшая степень равна
Теперь и числитель, и знаменатель имеют при
Пусть
При
Пример 5.Найти Решение. Степени многочленов Пример 6.Найти Решение. Раскрывая скобки, преобразуем числитель к виду
а знаменатель – к виду Получаем Пример 7.Найти Решение. Чтобы определиться со старшей степенью числителя и знаменателя, воспользуемся биномом Ньютона:
Неопределённость Пример 8.Вычислить Решение.
Пример 9.Вычислить Решение.
Пример 10.Вычислить Решение.
Поиск по сайту: |
 при стремлении аргумента
при стремлении аргумента  к
к  . После преобразования
. После преобразования
 , знак при
, знак при  зависит только от знака старшего коэффициента
зависит только от знака старшего коэффициента  , а при
, а при  - от знака
- от знака  .
. и
и 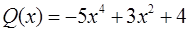 при стремлении аргумента
при стремлении аргумента  ,
, .
. ,
, .
. ,
, .
. ,
, опять определяет знак старшего коэффициента. ▲
опять определяет знак старшего коэффициента. ▲ всегда приводит к неопределённости вида
всегда приводит к неопределённости вида  .
. б)
б)  .
. :
: .
. неопределённости не осталось: теперь и числитель, и знаменатель по теореме о пределе суммы при
неопределённости не осталось: теперь и числитель, и знаменатель по теореме о пределе суммы при  имеют конечные пределы, причём предел знаменателя равен
имеют конечные пределы, причём предел знаменателя равен  . В силу теоремы о пределе частного
. В силу теоремы о пределе частного .
.
 .
.
 .
.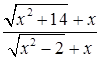 при
при  .
. ). После того, как разделим и числитель, и знаменатель на
). После того, как разделим и числитель, и знаменатель на 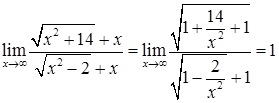 . ▲
. ▲ =
=  , в знаменателе старшая степень - тоже
, в знаменателе старшая степень - тоже  и числитель, и знаменатель:
и числитель, и знаменатель:
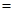
 .
. . В силу теоремы о пределе частного получаем
. В силу теоремы о пределе частного получаем  . ▲
. ▲ и
и  , тогда
, тогда
 этот результат был получен ранее, когда аргументом было натуральное число
этот результат был получен ранее, когда аргументом было натуральное число  , а не непрерывно изменяющаяся переменная
, а не непрерывно изменяющаяся переменная 
 и
и 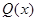 одинаковы, поэтому предел равен отношению коэффициентов при старших степенях. Так как в числителе слагаемое
одинаковы, поэтому предел равен отношению коэффициентов при старших степенях. Так как в числителе слагаемое  повторяется 10 раз, получаем
повторяется 10 раз, получаем  . ▲
. ▲ .
. ,
, .
.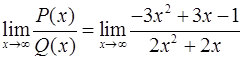 . Степени числителя и знаменателя одинаковы, поэтому предел равен отношению коэффициентов при старших степенях:
. Степени числителя и знаменателя одинаковы, поэтому предел равен отношению коэффициентов при старших степенях:  .▲
.▲
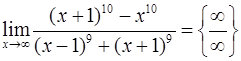 .
. ;
;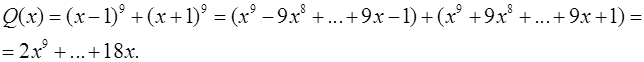 Оказалось,что степени многочленов
Оказалось,что степени многочленов  .▲
.▲ сводится к неопределённости
сводится к неопределённости  .
.
 . ▲
. ▲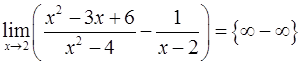 .
.
 . ▲
. ▲
 . ▲
. ▲