 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Ограниченные и неограниченные последовательности
Основной операцией математического анализа является операция предельного перехода.Сначала рассмотрим простейшую форму предельного перехода на примере числовой последовательности. Определение.Если каждому натуральному числу 1, 2,…, n,…поставлено в соответствие по определенному закону вещественное число будем называть числовой последовательностью. Числа Зная Таким образом, числовая последовательность - это функция, определенная на множестве натуральных чисел:
Пример 1.Выписать первые пять членов последовательности а) Решение. а)
б) Если если если
в) Если С другой стороны, так как каждый элемент последовательности строится по определенному закону, то, зная несколько первых членов последовательности, можно предположить, как выглядит её Пример 2.По нескольким первым членам последовательности записать её а) Решение. а) Знаменатели 3, 6, 9…образуют арифметическую прогрессию, первый член которой
б) Знаменатели 2,4,8,… изменяются по закону в) Запишем последовательность в виде Введем понятие арифметических операций над числовыми последовательностями. Пусть даны две последовательности Введем понятие ограниченной числовой последовательности. Само слово «ограниченная» предполагает существование границ, в пределах которых находятся все элементы последовательности. Определение.Последовательность Числа Данное определение можно записать в другой форме. Если обозначить через
Пример 3. Последовательность Если же последовательность не ограничена, то не существует границ, в пределах которых находились бы все элементы последовательности. Определение.Последовательность
Сравнивая определения ограниченной и неограниченной последовательности, замечаем, что кванторы Пример 4. Доказать, что последовательность Доказательство. Действительно каким бы большим ни было число Пример 5. Доказать, что последовательность Доказательство . Поскольку неравенство
Поиск по сайту: |
 , то множество занумерованных действительных чисел
, то множество занумерованных действительных чисел  ,
, 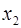 ,…,
,…, 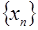 (иногда просто
(иногда просто 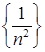 обозначает последовательность
обозначает последовательность  , а символ
, а символ 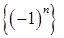 - последовательность
- последовательность  Множество значений последовательности может быть как конечным, так и бесконечным. Например, множество значений последовательности
Множество значений последовательности может быть как конечным, так и бесконечным. Например, множество значений последовательности  состоит из двух чисел 1 и –1, множество значений последовательности
состоит из двух чисел 1 и –1, множество значений последовательности  -й член последовательности, можно записать любой член последовательности.
-й член последовательности, можно записать любой член последовательности. .
.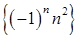 , б)
, б) 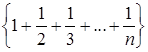 , в)
, в) 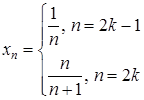
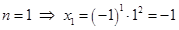 ;
; ;
;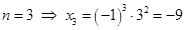 ;
;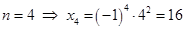 ;
;
 , то имеем одно слагаемое и
, то имеем одно слагаемое и 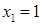 ;
; , то имеем два слагаемых и
, то имеем два слагаемых и 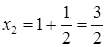 ;
;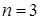 , то
, то 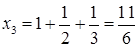 ;
;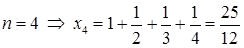 ;
;  .
.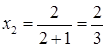 ; если
; если 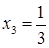 ;
; 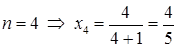 ;
; 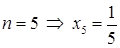 . ▲
. ▲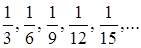 б)
б) 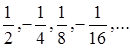 ; в)
; в)  ,
, , разность
, разность  . Значит,
. Значит,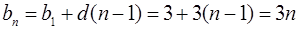 , тогда
, тогда 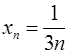 .
. , также происходит чередование знаков, начиная с «+». Значит,
, также происходит чередование знаков, начиная с «+». Значит, 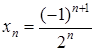 .
.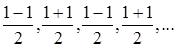 Первое слагаемое в числителе всегда равно 1; а знаки второго слагаемого чередуются, начиная с отрицательного, т.е. изменяются по закону
Первое слагаемое в числителе всегда равно 1; а знаки второго слагаемого чередуются, начиная с отрицательного, т.е. изменяются по закону 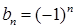 . Значит, числитель можно представить в виде
. Значит, числитель можно представить в виде  . Тогда
. Тогда 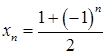 . ▲
. ▲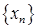 и
и 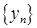 . Суммой этих последовательностей назовем последовательность
. Суммой этих последовательностей назовем последовательность 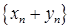 , разностью –
, разностью –  , произведением –
, произведением – 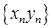 , частным –
, частным – 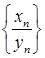 . Для существования последней последовательности необходимо потребовать, чтобы все элементы
. Для существования последней последовательности необходимо потребовать, чтобы все элементы  .
. называется ограниченной, если существуют такие числа
называется ограниченной, если существуют такие числа 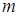 и
и 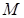 , что любой элемент
, что любой элемент 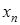 данной последовательности удовлетворяет неравенствам
данной последовательности удовлетворяет неравенствам 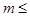
 .
.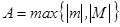 , тогда все элементы последовательности
, тогда все элементы последовательности 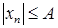 , иначе,
, иначе, 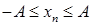 . Используя кванторы
. Используя кванторы 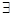 (существует, найдется) и
(существует, найдется) и 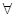 (любой, для любого), это определение коротко можно записать так:
(любой, для любого), это определение коротко можно записать так: (
(  ).
).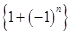 ограничена, так как
ограничена, так как 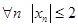 .
. найдется элемент
найдется элемент 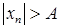 или короче
или короче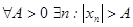 .
. и
и 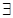 поменялись местами и знак неравенства изменился на противоположный.
поменялись местами и знак неравенства изменился на противоположный. не ограничена.
не ограничена. , обязательно найдётся (чётный) номер
, обязательно найдётся (чётный) номер 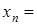
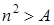 . ▲
. ▲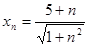 ограничена.
ограничена. очевидно для
очевидно для  , то
, то  . Тогда
. Тогда 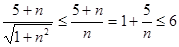 для всех номеров
для всех номеров 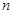 , начиная с первого. Значит,
, начиная с первого. Значит,  . А это в силу определения и означает ограниченность данной последовательности. ▲
. А это в силу определения и означает ограниченность данной последовательности. ▲