 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Метод математической индукцииСтр 1 из 4Следующая ⇒
Во многих разделах математики приходится доказывать истинность утверждений на множестве натуральных чисел. Часто это удается сделать методом математической индукции, в основе которого лежит Теорема.Пусть некоторое множество Пример 1. Докажем, что для любого натурального числа
Доказательство. Символом
Пусть 1. При 2. Делаем индукционный шаг. Пусть условие (1) выполняется для некоторого
Левая часть здесь – это
Таким образом,
Отсюда следует, что и Пример 2. Докажем, что для любого натурального числа
Доказательство. 1. Сначала проверим базис: при 2. Далее делаем индукционный шаг. Пусть для некоторого натурального числа
Но это и означает справедливость формулы (2) для Пример 3. Доказать, что при Доказательство. Положим
Так как каждое из слагаемых кратно 19, то Пример 4*. Доказать формулу (бином Ньютона)
Здесь обозначено Доказательство формулы (3) проведем методом математической индукции. Пусть
1. При 2. Делаем индукционный шаг. Пусть условие (2) выполняется для некоторого
Левая часть здесь – это Сначала разобьем правую часть на два слагаемых:
В сумме
А в сумме
Теперь справа в (4) получаем:
Здесь учтено, что Преобразуем выражение в скобках:
Теперь правая часть соотношения (4) принимает вид
Окончательно получим
А это означает, что и
Полезно запомнить формулу (3) и в развернутом виде:
Поиск по сайту: |
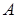 натуральных чисел
натуральных чисел  удовлетворяет следующим двум условиям: 1) 1
удовлетворяет следующим двум условиям: 1) 1  , 2) если
, 2) если  , то
, то  . Тогда множество
. Тогда множество 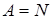 .
. имеет место равенство
имеет место равенство .(1)
.(1) обозначается сумма слагаемых вида
обозначается сумма слагаемых вида  , индекс суммирования
, индекс суммирования  – натуральное число – принимает значения от
– натуральное число – принимает значения от  до
до  :
: .
.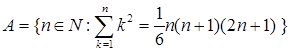 .
. условие (1) выполнено:
условие (1) выполнено:  , то есть
, то есть  (проверка базиса)
(проверка базиса) , оно остается справедливым и после прибавления к обеим частям слагаемого
, оно остается справедливым и после прибавления к обеим частям слагаемого 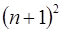 :
: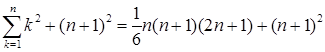 .
.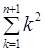 . Правая часть преобразуется к виду
. Правая часть преобразуется к виду

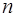 имеет место равенство (формула для суммы
имеет место равенство (формула для суммы  . (2)
. (2) .
.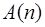 , т.е. равенство (2) справедливо; покажем, что отсюда следует и его справедливость для числа
, т.е. равенство (2) справедливо; покажем, что отсюда следует и его справедливость для числа  , следующего за
, следующего за 

 .
. . В силу метода математической индукции формула справедлива для любого натурального
. В силу метода математической индукции формула справедлива для любого натурального 
 число
число  кратно 19.
кратно 19. . При
. При  , очевидно, делится на 19. Предположим, что
, очевидно, делится на 19. Предположим, что 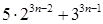 кратно 19. Подставим в это число
кратно 19. Подставим в это число  вместо
вместо  .
.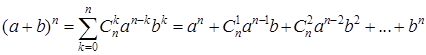 . (3)
. (3) – число сочетаний из
– число сочетаний из  . Например,
. Например,  . Действительно, из трех элементов
. Действительно, из трех элементов  можно составить три сочетания по два элемента:
можно составить три сочетания по два элемента:  . Вычислим еще
. Вычислим еще 
 , тут
, тут 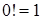 по определению.
по определению. .
. . Значит,
. Значит,  :
: . (4)
. (4)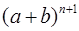 . Покажем, что правую часть соотношения (4) можно преобразовать к виду
. Покажем, что правую часть соотношения (4) можно преобразовать к виду 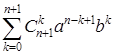 .
.
 выделим первое слагаемое и запишем её в виде:
выделим первое слагаемое и запишем её в виде:

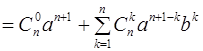 .
. выделим последнее слагаемое и запишем её в виде:
выделим последнее слагаемое и запишем её в виде: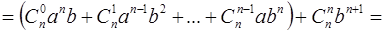
 .
.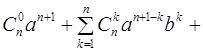
 =
=
 .
.

 ,
,
 .
.