 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Возрастание и убывание функций
Функция f (x) называется возрастающей (неубывающей) на интервале (a,b), если Функция f (x) называется убывающей (невозрастающей) на интервале (a,b), если Теорема 1. Пусть f (x) дифференцируема на (a,b). Тогда если Замечание 1. Условие Интервалы возрастания и убывания функции называются интервалами монотонности. Точки экстремума функций. Необходимое и достаточное условия существования экстремума функции Точка Теорема 1. (Необходимое условие экстремума). Пусть т. Теорема 2. (Достаточное условие экстремума). Пусть либо а) Пример. Найти интервалы монотонности и точки экстремума функции Ñ
-1 1/2 5 Например, Пример. Найти соотношение между радиусом R и высотой H цилиндра, имеющего при данном объеме V наименьшую полную поверхность S. ÑФормула площади полной поверхности имеет вид
  _ _  + +
При Пусть Пример. Найти наибольшее и наименьшее значения
Заметим что,
Поиск по сайту: |
 таких, что
таких, что  выполняется
выполняется 
 .
. ,
, 
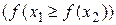 .
.

 , то f (x) возрастающая (убывающая) на (a,b).
, то f (x) возрастающая (убывающая) на (a,b).
 является необходимым и достаточным для неубывания (невозрастания) f (x) на (a,b).
является необходимым и достаточным для неубывания (невозрастания) f (x) на (a,b). называется точкой локального максимума (локального минимума) функции
называется точкой локального максимума (локального минимума) функции 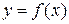 , если
, если 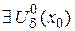 - проколотая окрестность т.
- проколотая окрестность т. 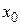 такая что
такая что 

 . Точки локального максимума и локального минимума называются точками экстремума функции.
. Точки локального максимума и локального минимума называются точками экстремума функции. либо
либо  не существует.
не существует. непрерывна в т.
непрерывна в т.  . Тогда, если выполняются следующие условия:
. Тогда, если выполняются следующие условия: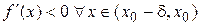 ,
, 
 , либо б)
, либо б)  ,
,  , то
, то  .
. . Вычислим производную.
. Вычислим производную.  = =
= =  . Экстремум может достигаться при
. Экстремум может достигаться при  ,
,  и
и  , так как эти значения принадлежат области определения
, так как эти значения принадлежат области определения  ,
,  .
.






 . По методу интервалов получаем остальные знаки. Тогда
. По методу интервалов получаем остальные знаки. Тогда 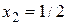 - точка локального максимума функции.#
- точка локального максимума функции.# . Так как
. Так как  , то выразив
, то выразив  можно получить
можно получить  . Исследуем S (R) на экстремум.
. Исследуем S (R) на экстремум.  . Экстремум возможен если
. Экстремум возможен если  т.е.
т.е. 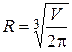 . Проверим смену знаков
. Проверим смену знаков 




 0
0 . #
. # и точки
и точки 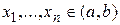 такие что
такие что  ,
,  либо равна 0, либо не
либо равна 0, либо не  . Тогда наибольшее значение
. Тогда наибольшее значение  , а наименьшее -
, а наименьшее - 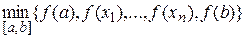 .
. на [0, 1]. Ñ Вычислим производную:
на [0, 1]. Ñ Вычислим производную: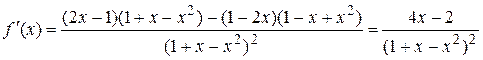 .
. на [0, 1]. Экстремум возможен при
на [0, 1]. Экстремум возможен при 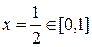 . Тогда fнаибольшее=
. Тогда fнаибольшее=  , fнаименьшее=
, fнаименьшее=  . Здесь наибольшее значение достигается в двух точках, а наименьшее – в одной. #
. Здесь наибольшее значение достигается в двух точках, а наименьшее – в одной. #