 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задачи для самостоятельного решения. Доказать, что указанные функции являются монотонно возрастающими (убывающими) в
Доказать, что указанные функции являются монотонно возрастающими (убывающими) в указанных промежутках. 34. 36. 38.
Четные и нечетные функции.Функция Пример.а) Пример. Доказать, что всякую функцию, определенную в Ñ =
Задачи для самостоятельного решения
39. Какие из указанных ниже функций четны, какие нечетны, какие не являются ни четными, ни нечетными? a) д) з) Представить в виде суммы четной и нечетной функций: 40. 42. Доказать, что произведение двух четных функций есть четная функция, произведение двух нечетных – четная функция, произведение четной и нечетной – нечетная функция. Периодические функции.Функция
Наименьшее из T , для которых выполняется (2.2) называется периодом Пример. Найти, если существует, период функции Ñ Функция определена Функции Теорема 1.1. Если функция Доказательство. 1) По определению (2.2):
где Пусть функция 2) Доказать самостоятельно. Пример. Будет ли периодической функция Ñ Функции
Задачи для самостоятельного решения
Выяснить, какие из нижеследующих функций будут периодическими, и определить период. 43. 47. 50. Построить график периодической функции с периодом 51. Доказать методом полной индукции: если T- период функции
Обратная функция Пусть двум любым различным элементам множества D соответствуют по закону f два различных элемента множества E. Тогда говорят, что между D и E установлено взаимно однозначное соответствие. Отображение Пусть даны непустые множества Функцию g будем называть обратной к функции f , если для всякого выполняется
и для всякого
Функция g, обратная к f, обозначается Теорема 1.2. Если функция f строго монотонна в области X и имеет область значений Y, то для нее существует однозначная обратная функция Если непрерывная функция не является строго монотонной во всей своей области определения, то, если возможно, область определения разбивают на интервалы, в которых функция строго монотонна, и в каждом таком интервале справедлива теорема 1.2. Для функций, заданных аналитически Пример. Найти обратную функцию для функции Ñ Если областью определения функции а) б) Взаимно обратными функциями являются, например, а) б) в) г) д)
Поиск по сайту: |
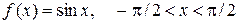 . 35.
. 35. 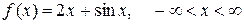 .
.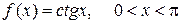 .
. .
. , определенная в симметричном интервале
, определенная в симметричном интервале  , называется четной, если
, называется четной, если  , и нечетной, если
, и нечетной, если  .
.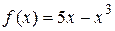 ,
, 

 , - функция
, - функция  ,
, 
 ,- функция g(x) – четная.
,- функция g(x) – четная.
 , где
, где  ,
,  ;
; , значит,
, значит, 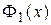 - четная,
- четная, , значит,
, значит,  - нечетная. #
- нечетная. # , б)
, б)  , в)
, в)  , г)
, г)  ,
, , е)
, е) 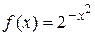 , ж)
, ж)  ,
, , и)
, и)  .
. , 41.
, 41. 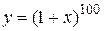 .
. выполняется
выполняется (2.2)
(2.2) - период функции в широком смысле слова.
- период функции в широком смысле слова. (
(  ).
). . По определению
. По определению  ,
,  - уравнение для определения T; преобразуем его:
- уравнение для определения T; преобразуем его:  . Так как x- любое из R, то последнее уравнение выполняется, если
. Так как x- любое из R, то последнее уравнение выполняется, если  , отсюда
, отсюда  ,
,  . Наименьшее (отличное от нуля) T получим при
. Наименьшее (отличное от нуля) T получим при  . #
. # имеют период
имеют период 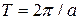 , функции
, функции  - период
- период  .
. имеет период
имеет период  , а
, а  , определенная в
, определенная в  - период
- период  , то: 1) определенная в
, то: 1) определенная в  функция
функция  будет периодической с периодом T, если отношение
будет периодической с периодом T, если отношение  - рациональное число; 2) период T – наименьшее общее кратное чисел
- рациональное число; 2) период T – наименьшее общее кратное чисел 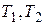 .
. ,
,  , (2.3)
, (2.3) - целые.
- целые.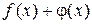 - периодическая с периодом T, тогда по определению (2.2)
- периодическая с периодом T, тогда по определению (2.2)  , отсюда с учетом (2.3) следует
, отсюда с учетом (2.3) следует  или
или 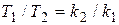 . При целых
. При целых  - рациональное число.
- рациональное число. ?
? и
и  определены
определены  и
и 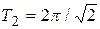 соответственно. Тогда y определена
соответственно. Тогда y определена  - иррациональное (трансцендентное) число, то функция
- иррациональное (трансцендентное) число, то функция 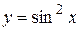 , 44.
, 44.  , 45.
, 45.  , 46.
, 46.  ,
,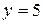 , 48.
, 48.  , 49.
, 49.  .
.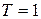 , которая на промежутке
, которая на промежутке 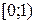 задана формулой: а)
задана формулой: а)  , б)
, б) 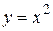 .
. , где
, где  .
. называется обратной функцией по отношению к
называется обратной функцией по отношению к 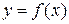 и обозначается
и обозначается  или
или  . Если учесть, что традиционно функцию обозначают y а аргумент x, то обратной функцией к
. Если учесть, что традиционно функцию обозначают y а аргумент x, то обратной функцией к  .
.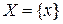 и
и  и функции
и функции  и
и 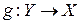 , при этом функция f двум разным значениям
, при этом функция f двум разным значениям  и
и  из X ставит в соответствие разные значения
из X ставит в соответствие разные значения  и
и  из Y.
из Y.

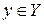 выполняется
выполняется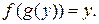
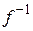 . Если учесть, что традиционно функцию обозначают y а аргумент x, то обратной функцией к
. Если учесть, что традиционно функцию обозначают y а аргумент x, то обратной функцией к  , обратную функцию можно получить, выразив x через y, затем, следуя традиции, условимся менять x и y местами.
, обратную функцию можно получить, выразив x через y, затем, следуя традиции, условимся менять x и y местами. функция убывает, на
функция убывает, на  - возрастает, и однозначно определенной обратной функции нет. Но на интервалах монотонного изменения функции
- возрастает, и однозначно определенной обратной функции нет. Но на интервалах монотонного изменения функции  т.е. обратная функция
т.е. обратная функция  ;
; , т.е. обратная функция
, т.е. обратная функция  .#
.#

 ;
; ,
, 
 ;
;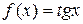 ,
, 
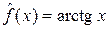 ;
; ,
, 
 ;
;

 .
.