 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Лекция 3.4 «Определенный интеграл»
Вопросы: 1.Определение, геометрический и экономический смысл определенного интеграла. Функция f (х) задана на отрезке [a, b]. Разобьем отрезок на n произвольных частей точкам Геометрический смысл интегральной суммы: это сумма площадей прямоугольников с основаниями Sn зависит от способа разбиения отрезка [a, b] и от выбора точек ξi. Будем менять разбиение {x0, x1, …, xn}. Следовательно, получим последовательность разбиений, которой будет соответствовать последовательность Определение. Пусть предел I интегральной суммы Sn при Не имеет значения, какой буквой обозначена переменная интегрирования определенного интеграла Во введенном определении определенного интеграла предполагается, что a<b. Тогда Свойства: 1). 2). 3). Если функции f (х) и g(x) – интегрируемы на отрезке [a, b], то функция f (х) ± g (x) также интегрируема на отрезке [a, b], при этом 4). Если функция f (х) – интегрируема на отрезке [a, b], k – число, то функция kf (х) – также интегрируема на отрезке [a, b], при этом 5). Если функция f (х) – интегрируема на отрезках [a, с] и [с, b], (a<c<b), то функция f (х) – интегрируема на отрезке [a, b], и наоборот. При этом 6). Если функция f (х) ≥0 на отрезке [a, b], a<b, то 7). Если функции f (х) и g(x) удовлетворяют неравенству f (х) ≤ g (x) на отрезке [a, b], a<b, то 8). Если функция f (х) – интегрируема на отрезке [a, b], a<b, то │ 9). Если М – max, m – min функции f (х) на отрезке [a, b], a<b, то m (b-a) ≤ 10. Теорема о среднем значении для определенного интеграла. Если функция f (х) – непрерывна на отрезке [a, b], a<b, то существует такая точка с Пусть функция f (х) ≥0 на отрезке [a, b], где a<b. Тогда Теорема. Пусть функция f (х) непрерывна на отрезке [a, b] и F(х) – первообразная для f (х). Тогда Пример. Интегрирование по частям. Пример. Замена переменной в определенном интеграле. Теорема. Пусть функция f (х) непрерывна на отрезке [a, b], а функция Пример. = Т1. Если функция f (х) непрерывна на отрезке [a, b], то она интегрируема на нем. Т2. Если определенная и ограниченная на множестве [a, b] функция f (х) имеет конечное число точек разрыва первого рода, то она интегрируема на этом отрезке. Т3. Монотонная на отрезке [a, b] функция f (х) интегрируема на этом отрезке. Вообще говоря, в экономических задачах переменные меняются дискретно. Для использования определенного интеграла нужно составить некоторую идеализированную модель, предполагающую непрерывное изменение зависимых и независимых переменных. Несмотря на то, что эти задачи содержательно не связаны между собой, с математической точки зрения они сходны. В микро экономике часто приходится находить саму функцию по известной ее предельной величине (производной f /(x)), т.е. решать задачу обратную нахождению производной данной функции – задачу интегрирования функции.
Поиск по сайту: |
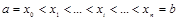 . Выберем в каждом множестве [xi-1, xi] произвольную точку ξi. Составим сумму произведений
. Выберем в каждом множестве [xi-1, xi] произвольную точку ξi. Составим сумму произведений  , которою будем называть интегральной суммой (сумма Римана).
, которою будем называть интегральной суммой (сумма Римана). и высотами
и высотами  , i=1,2,…n.
, i=1,2,…n.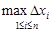 и последовательность интегральных сумм Sn. Пусть при некоторой выбранной последовательности разбиений, когда
и последовательность интегральных сумм Sn. Пусть при некоторой выбранной последовательности разбиений, когда  , эта сумма Sn стремится к пределу I.
, эта сумма Sn стремится к пределу I. , а сама функция называется интегралом на отрезке [a, b], т.е.
, а сама функция называется интегралом на отрезке [a, b], т.е.  =
= 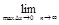
 =I. При этом число а – нижний предел интегрирования, b – верхний предел интегрирования, f (х) – подынтегральная функция, f (х) dx – подынтегральное выражение.
=I. При этом число а – нижний предел интегрирования, b – верхний предел интегрирования, f (х) – подынтегральная функция, f (х) dx – подынтегральное выражение.  =
=  .
.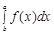 . Если a = b,
. Если a = b,  =0.
=0.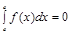 .
. =
=  .
.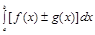 =
=  .
. =
=  .
.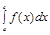 +
+  .
.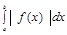 .
.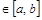 , что интеграл
, что интеграл  = F(b)-F(a). (Формула Ньютона-Лейбница).
= F(b)-F(a). (Формула Ньютона-Лейбница). =
= 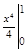 = ¼ – 0 = ¼.
= ¼ – 0 = ¼. .
.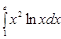 =
=  =
= 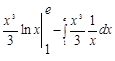 =
=  - -
- -  =
=  .
. определена на отрезке
определена на отрезке  и имеет непрерывную производную внутри этого отрезка, причем
и имеет непрерывную производную внутри этого отрезка, причем 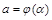 ,
, 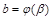 . Тогда
. Тогда 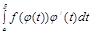 .
. =
=  =
=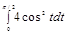 = 2
= 2  =π.
=π.