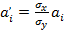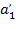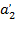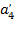|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Линейная множественная регрессия
Так как множественный коэффициент детерминации равен 0,964312164, то вариация результативного признака обусловлена в основном влиянием включенных в регрессионную модель факторов. То есть выбранные причинные факторы существенно влияют на «Промышленное производство», что подтверждает правильность включения этих факторов в модель.
Рассчитанный уровень значимости
Из полученных данных получается уравнение регрессии:
В множественной регрессии коэффициенты причинных факторов являются размерными, поэтому полученные коэффициенты не могут отражать степень влияния каждого фактора. Чтобы получить уравнение регрессии необходимо преобразовать размерные коэффициенты в безразмерные, которые будут отражать степень влияния.
где В результате вычислений получились следующие безразмерные коэффициенты:
Теперь подставим рассчитанные ранее безразмерные коэффициенты в формулу
Проанализировав данное уравнение можно сделать вывод о том, что наиболее сильное влияние на результативный фактор «Промышленное производство» оказывает причинный фактор «Обработка древесины», а наименьшее (незначительное) влияние оказывает «Текстильное и швейное производство».
Окончательное уравнение примет вид:
Проанализировав график значений фактического и предсказанного промышленного производства, можно говорить о том, что они приблизительно равны. Из этого следует то, что данную модель можно применять на практике
Поиск по сайту: |
 = 5,30083E-11< 0,05 (показатель Значимость) подтверждает значимость R
= 5,30083E-11< 0,05 (показатель Значимость) подтверждает значимость R
 ,
,