Определение параметров описательной статистики

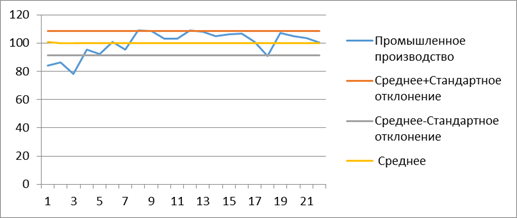
В данном разделе будут рассмотрены параметры описательной статистики для каждого параметра исходной таблицы. Так же для каждого параметра будет рассчитан коэффициент вариации.

На основании проведенного обследования параметра «Промышленное производство» и рассчитанных по данной выборке показателей описательной статистики (Таблица 6), с уровнем надежности 95% можно предположить, что параметр стационарен, так как коэффициент вариации меньше 50%. График функции распределения будет островершинным, так как эксцесс больше нуля и ассиметричным со смещением влево, так как асимметричность меньше нуля. Площадь, ограничивающаяся кривой распределения делится пополам в точке Me=103. Среднее квадратическое отклонение от среднего (стандартная ошибка) равна 1,87.

Таблица 6 "Оп. статистика промышленного производства"

Значения случайных величин индекса промышленного производства отклонялись от математического ожидания (среднего) в пределах от 91,1 до 108,7. Наглядно это можно увидеть на графике ниже:

На основании проведенного обследования параметра «Добыча полезных ископаемых» и рассчитанных по данной выборке показателей описательной статистики (Таблица 7), с уровнем надежности 95% можно предположить, что параметр стационарен, так как коэффициент вариации меньше 50%. График функции распределения будет островершинным, так как эксцесс больше нуля и ассиметричным со смещением влево, так как асимметричность меньше нуля. Площадь, ограничивающаяся кривой распределения делится пополам в точке Me=101,25. Среднее квадратическое отклонение от среднего (стандартная ошибка) равна 1,16.

Таблица 7 "Оп. статистика добычи полезных ископаемых"

Значения случайных величин индекса добычи полезных ископаемых отклонялись от математического ожидания (среднего) в пределах от 95,2 до 106,2. Наглядно это можно увидеть на графике ниже:

На основании проведенного обследования параметра «Производство пищевых продуктов» и рассчитанных по данной выборке показателей описательной статистики (Таблица 8), с уровнем надежности 95% можно предположить, что параметр стационарен, так как коэффициент вариации меньше 50%. График функции распределения будет островершинным, так как эксцесс больше нуля и ассиметричным со смещением влево, так как асимметричность меньше нуля. Площадь, ограничивающаяся кривой распределения делится пополам в точке Me=103,55. Среднее квадратическое отклонение от среднего (стандартная ошибка) равна 1,9.

Таблица 8 "Оп. статистика производства пищевых продуктов"

Значения случайных величин индекса производства пищевых продуктов отклонялись от математического ожидания (среднего) в пределах от 91,4 до 109,3. Наглядно это можно увидеть на графике ниже:

Изучив данные описательной статистики по параметру «Текстильное и швейное производство» (Таблица 9), можно сказать, что параметр стационарен, так как коэффициент вариации меньше 50%. График функции распределения будет островершинным, так как эксцесс больше нуля и ассиметричным со смещением влево, так как асимметричность меньше нуля. Площадь, ограничивающаяся кривой распределения делится пополам в точке Me=100,1. Среднее квадратическое отклонение от среднего (стандартная ошибка) равна 3,5.

Таблица 9 "Оп. статистика текстильного и швейного производства"

Значения случайных величин индекса текстильного и швейного производства отклонялись от математического ожидания (среднего) в пределах от 79 до 111,9. Наглядно это можно увидеть на графике ниже:

Изучив данные описательной статистики по параметру «Обработка древесины» (Таблица 10), можно сказать, что параметр стационарен, так как коэффициент вариации меньше 50%. График функции распределения будет плосковершинным, так как эксцесс больше нуля и ассиметричным со смещением влево, так как асимметричность меньше нуля. Площадь, ограничивающаяся кривой распределения делится пополам в точке Me=101,75. Среднее квадратическое отклонение от среднего (стандартная ошибка) равна 2,82.

Таблица 10 "Оп. статистика обработки древесины"

Значения случайных величин индекса обработки древесины отклонялись от математического ожидания (среднего) в пределах от 85,1 до 111,6. Наглядно это можно увидеть на графике ниже:

Изучив данные описательной статистики по параметру «Химическое производство» (Таблица 11), можно сказать, что параметр стационарен, так как коэффициент вариации меньше 50%. График функции распределения будет островершинным, так как эксцесс больше нуля и ассиметричным со смещением влево, так как асимметричность меньше нуля. Площадь, ограничивающаяся кривой распределения делится пополам в точке Me=104,1. Среднее квадратическое отклонение от среднего (стандартная ошибка) равна 2,51.

Таблица 11 "Оп. статистика химического производства"

Значения случайных величин индекса химического производства отклонялись от математического ожидания (среднего) в пределах от 89,24 до 112,80. Наглядно это можно увидеть на графике ниже:

Поиск по сайту: