 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Диференціальне формулювання закону Джоуля-Ленца ⇐ ПредыдущаяСтр 5 из 5
Як і для закону Ома, візьмемо трубку струму силою
Знаки ми врахували, знаючи, що
де Введемо диференціальну величину
що дорівнює кількості тепла, яка виділяється за 1 секунду в одиниці об’єму. В загальному випадку та для анізотропних речовин, коли
Для ізотропного середовища
закон Джоуля-Ленца в диференціальній формі. Як і для закону Ома, ці диференціальні співвідношення можна використати, коли
Сторонні е.р.с.
Давайте порівняємо процеси створення електростатичного поля і протікання струму. Електростатичне поле вимагає втрати енергії тільки при його створенні. Протікання постійного струму супроводжується неперервним виділенням тепла Джоуля-Ленца і, відповідно, неперервним втратам енергії. Ці втрати повинні неперервно ж відшкодовуватись за рахунок інших видів енергії – механічної (динамо-машина), хімічної (гальванічні елементи, акумулятори), теплової (термоелементи), тощо. Це означає, що в колі постійного струму повинні існувати джерела енергії, які використовують некулонівські, так звані сторонні сили. Наявність сторонніх сил означає, що у всьому колі постійного струму, або в якійсь його частині, на носій струму, крім кулонівського поля
З урахуванням поля сторонніх сил, закон Ома ми повинні записати у вигляді
При цьому поле сторонніх сил Свого часу ми вводили різницю потенціалів двох точок 1 і 2 як роботу кулонівського поля по переміщенню одиничного позитивного точкового заряду з точки 1 до точки 2
Аналогічно введемо роботу сторонніх сил по переміщенню заряду з точки 1 в точку 2
і назвемо цю величину електрорушійною силою (е.р.с.).
Помножимо скалярно на
поділимо на
і проінтегруємо від 1 до 2
За означеннями
в лівій частині помножимо чисельник і знаменник під знаком інтегралу на площу перерізу
де
звідки
маємо закон Ома для ділянки кола з урахуванням е.р.с. Отже, добуток сили струму на опір довільної ділянки провідника дорівнює сумі падіння напруги та сторонньої е.р.с., прикладених до цієї ділянки.
Поиск по сайту: |
 довжиною
довжиною  з площею перерізу
з площею перерізу 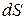 і падінням напруги
і падінням напруги 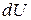 . Тоді
. Тоді .
. і що
і що  . Тоді
. Тоді ,
, об’єм трубки.
об’єм трубки. ,
, тензор, і вектор
тензор, і вектор 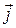 не паралельний вектору
не паралельний вектору 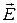 , маємо
, маємо .
.
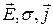 змінюються від точки до точки.
змінюються від точки до точки. . Поділивши ці сили на заряд носія струму
. Поділивши ці сили на заряд носія струму  , отримаємо напруженість поля сторонніх сил
, отримаємо напруженість поля сторонніх сил .
. .
. може існувати як у всьому колі, так і на будь-якій його ділянці.
може існувати як у всьому колі, так і на будь-якій його ділянці. .
.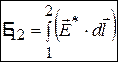 .
. Візьмемо тепер яку-небудь ділянку кола постійного струму від точки 1 до точки 2. На цій ділянці можуть діяти е.р.с., а еквівалентний опір ділянки
Візьмемо тепер яку-небудь ділянку кола постійного струму від точки 1 до точки 2. На цій ділянці можуть діяти е.р.с., а еквівалентний опір ділянки  (опір всього, що на ній є). Запишемо закон Ома для цієї ділянки
(опір всього, що на ній є). Запишемо закон Ома для цієї ділянки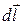
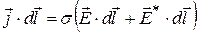 ,
,

 .
. ;
;  .
. , яка нормальна до вектора
, яка нормальна до вектора  ,
, ,
,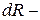 опір ділянки довжиною
опір ділянки довжиною 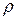 і
і  (нагадую, що ми розглядаємо постійний струм). В результаті маємо
(нагадую, що ми розглядаємо постійний струм). В результаті маємо ,
,