 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Залежність питомого опору від температури
Питомий опір Залежність питомого опору від температури характеризують температурним коефіцієнтом опору даної речовини
який являє собою відносну зміну питомого опору при зміні температури на 1 градус. У загальному випадку температурний коефіцієнт опору залежить від температури. Однак для великого класу провідників, до якого належать всі метали, зміна Якщо температурний коефіцієнт опору майже сталий, можна визначити за ним опір провідника при різних температурах. Виведемо цю формулу, звернувши увагу на ті допущення, при яких вона справедлива. Припустимо, що температурний коефіцієнт опору не залежить від температури
Тоді, проінтегрувавши рівняння
одержимо
Нехай при температурі плавлення льоду
звідки
Тоді температурна залежність питомого опору набуває вигляду
де Якщо припустити, що температурний інтервал настільки малий, що
Тоді
і остаточно
Залежність опору провідників від температури використовують у різних вимірювальних приладах. Найважливішим є термометр опору (термометр сопротивления). Він являє собою опір із платинової дротини, який вмикають у одне з плечей мостової схеми. Опір платини добре вивчений у широкому інтервалі температур і дуже сталий у часі. Тому, вимірюючи опір платинової дротини, можна дуже точно виміряти і температуру. Термометри опору мають і ту перевагу перед рідинними термометрами, що можуть працювати і при дуже високих, і при дуже низьких температурах, при яких рідинні термометри працювати не можуть.
Закон Джоуля-Ленца
З протіканням струму у провіднику нероздільно пов’язане виділення тепла (тобто нагрівання провідника) – це відомо вам зі школи.
Виділимо у провіднику ділянку між точками 1 і 2. Якщо сила струму у провіднику становить Робота електричних сил, що виконується при протіканні струму, дорівнює
де
скориставшись означенням напруги (або різниці потенціалів). Згідно закону збереження енергії, еквівалентна цій роботі кількість енергії повинна виділитись у вигляді іншої форми енергії, наприклад, у вигляді теплоти (хоч
звідки
Отримана формула виражає собою закон Джоуля-Ленца. Він означає, що якщо провідник не рухається, і в ньому не відбуваються хімічні реакції (як в електролітах), то струм виділяє енергію у вигляді тепла. Скориставшись законом Ома, вираз для кількості теплоти можна записати у вигляді
Введена таким чином кількість теплоти дорівнює кількості енергії, що виділяється за одиницю часу, і має назву Ватт. Її розмірність в системі СІ 1 Вт = 1 Дж/с = 1 В × 1 А = 1/300 од. напруги CGSE × 3×109 од. напруги CGSE = 107 ерг/с.
Поиск по сайту: |
 залежить не тільки від роду речовини. Експерименти показали, що питомий опір залежить і від температури. Для металів із зростанням температури
залежить не тільки від роду речовини. Експерименти показали, що питомий опір залежить і від температури. Для металів із зростанням температури  ,
, з температурою не дуже велика.
з температурою не дуже велика. .
. ,
, .
. питомий опір
питомий опір  , тоді
, тоді ,
, .
. ,
, температура за шкалою Цельсія.
температура за шкалою Цельсія. , то можна записати
, то можна записати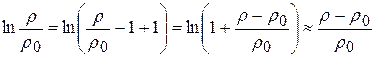 .
.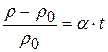 ,
, .
.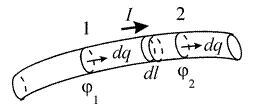 Кількість теплоти
Кількість теплоти  , що виділяється струмом за одиницю часу на виділеній ділянці провідника, може бути визначена наступним чином.
, що виділяється струмом за одиницю часу на виділеній ділянці провідника, може бути визначена наступним чином.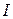 , то через будь-який переріз провідника протікає
, то через будь-який переріз провідника протікає  одиниць заряду. Тобто, якщо через переріз 1 пройде кількість заряду
одиниць заряду. Тобто, якщо через переріз 1 пройде кількість заряду  , то й через переріз 2 – теж
, то й через переріз 2 – теж  ,
,
 проекція вектора напруженості електричного поля на вектор зміщення
проекція вектора напруженості електричного поля на вектор зміщення 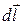 , перпендикулярний перерізу провідника в заданій точці. Скориставшись виразом
, перпендикулярний перерізу провідника в заданій точці. Скориставшись виразом  ,
,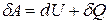 , зміною внутрішньої енергії нехтуємо). Отже, за час
, зміною внутрішньої енергії нехтуємо). Отже, за час  виділиться кількість теплоти
виділиться кількість теплоти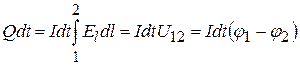 ,
,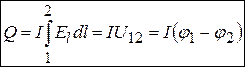 .
. .
.