|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Рівняння неперервності та умови стаціонарності струму
Подібно до того, як в електростатиці ми розглядали потік вектора напруженості електричного поля Візьмемо деяку замкнуту поверхню
а отже вираз
можна розглядати як кількісне інтегральне формулювання закону збереження заряду. Якщо заряд розповсюджений по об’єму, то закон збереження заряду можна записати як
Якщо об’єм не змінюється в часі, можна знак похідної внести під знак інтегралу і замінити її частинною похідною по часу (частинною тому, що величина змінюється за кількома змінними)
Скористаємось формулою Остроградського і замінимо інтеграл по поверхні інтегралом по об’єму
Якщо рівність інтегралів
не змінюється при зміні меж інтегрування, то рівними є підінтегральні вирази
Ми отримали диференціальну форму запису закону збереження заряду, або так зване рівняння неперервності (уравнение непрерывности). В цьому розділі ми будемо розглядати постійний електричний струм, тобто струм, який не залежить від часу. Зокрема це означає, що густина заряду
формулювання закону збереження заряду в диференціальній формі для постійного струму. Це рівняння є найбільш загальним виразом того факту, що постійний струм не має джерел і стоків, тобто лінії струму завжди замкнуті або йдуть на нескінченність (порівняйте із силовими лініями електростатичного поля : вони завжди починаються і закінчуються на зарядах). Оскільки
– закон збереження заряду в інтегральній формі для постійного струму. Тобто потік вектора густини струму через замкнуту поверхню дорівнює нулю, а це, з іншого боку, означає : скільки струму втікає у виділений об’єм, стільки й витікає.
Поиск по сайту: |
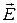 через замкнуту поверхню, розглянемо питання про силу струму
через замкнуту поверхню, розглянемо питання про силу струму 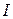 , або про потік вектора густини струму
, або про потік вектора густини струму 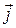 через замкнуту поверхню. При цьому треба враховувати, що експериментально не було виявлено таких процесів, при яких би електричний заряд виникав або зникав. Навіть якщо ці заряди виникають або зникають, то тільки парами, в склад яких входить позитивний та рівний йому негативний заряд (наприклад, електрон і позитрон). Тому один із основних фізичних законів – закон збереження заряду – говорить : електричний заряд не зникає і не виникає, повна величина заряду зберігається. Іноді цей закон формулюють так: заряд Всесвіту незмінний. Закон збереження заряду не означає, однак, що заряд всередині деякої замкненої поверхні не змінюється. Але єдиною причиною цього може бути прихід або вихід заряду через замкнену поверхню, тобто струм.
через замкнуту поверхню. При цьому треба враховувати, що експериментально не було виявлено таких процесів, при яких би електричний заряд виникав або зникав. Навіть якщо ці заряди виникають або зникають, то тільки парами, в склад яких входить позитивний та рівний йому негативний заряд (наприклад, електрон і позитрон). Тому один із основних фізичних законів – закон збереження заряду – говорить : електричний заряд не зникає і не виникає, повна величина заряду зберігається. Іноді цей закон формулюють так: заряд Всесвіту незмінний. Закон збереження заряду не означає, однак, що заряд всередині деякої замкненої поверхні не змінюється. Але єдиною причиною цього може бути прихід або вихід заряду через замкнену поверхню, тобто струм.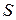 . Нехай заряд всередині цієї поверхні становить
. Нехай заряд всередині цієї поверхні становить 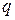 . Цей заряд може змінюватись в часі
. Цей заряд може змінюватись в часі 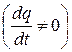 , але тільки завдяки струмові
, але тільки завдяки струмові 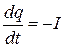 . Знак (–) в цьому співвідношенні пов’язаний з тим, що коли заряд
. Знак (–) в цьому співвідношенні пов’язаний з тим, що коли заряд 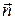 . Тобто, напрямок струму і напрямок руху електронів – протилежні. Тоді
. Тобто, напрямок струму і напрямок руху електронів – протилежні. Тоді
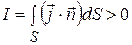 ,
,
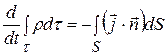 .
. .
. .
.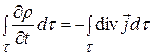
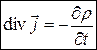 або
або 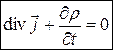 .
. стала у часі величина, і
стала у часі величина, і 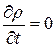 . Тоді із закону збереження заряду випливає
. Тоді із закону збереження заряду випливає
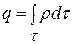 , то і заряд не залежить від часу. Звідси маємо
, то і заряд не залежить від часу. Звідси маємо