 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Одноэлектронное приближение
Многоэлектронная задача (решение уравнения (4.2)) может быть сведена к одноэлектронной. Для этого используют метод Харти-Фока, который состоит в замене потенциальной энергии взаимодействия электронов в уравнении (4.2) потенциальной энергией вида Это поле характеризует действие всех остальных электронов на i – ый электрон. Тогда уравнение Шредингера принимает вид: то есть гамильтониан системы представляет теперь сумму гамильтонианов отдельных электронов. Решением (4.3) является функция Каждая в котором взаимодействие i-го электрона с остальными описывается потенциалом Таким образом, введение эффективного поля позволяет свести многоэлектронное уравнение к системе одноэлектронных. При этом энергия системы Функция (4.4) является решением уравнения Шредингера для кристалла, однако не удовлетворяет принципу Паули. Согласно принципу Паули, в одном квантовом состоянии, характеризуемом волновой функцией Эту функцию записывают в виде определителя Слэтера:
N-число электронов, q обозначает набор трех пространственных координат и проекций спина, множитель Антисимметричные свойства вытекают из свойств определителя. Обозначим потенциальную энергию электрона в кристалле и запишем уравнение Шредингера в виде Атомы в кристалле расположены строго периодически, поэтому полный потенциал кристалла должен обладать трехмерной периодичностью. Функции Блоха Блохом было доказано, что волновые функции, являющиеся решениями одноэлектронного уравнения Шредингера с периодическим потенциалом, имеющим период решетки, представляют собой плоские волны, модулированные некоторой функцией с периодичностью решетки:
Здесь Условия периодичности потенциальной энергии в кристалле где где При смещении кристалла на Из условия трансляционной симметрии следует, что волновая функция электрона
Из условия нормировки Это условие можно удовлетворить, положив где Тогда из выражения (4.6) получаем: или где Таким образом, волновая функция электрона в кристалле представляет собой бегущую волну · модулированную периодической функцией · и зависящей от волнового вектора Функция
Поиск по сайту: |
 , представляющей собой энергию взаимодействия i-го электрона с некоторымэффективным полем, в котором каждый электрон движется независимо.
, представляющей собой энергию взаимодействия i-го электрона с некоторымэффективным полем, в котором каждый электрон движется независимо. , (4.3)
, (4.3) . (4.4)
. (4.4) удовлетворяет одноэлектронному уравнению Шредингера
удовлетворяет одноэлектронному уравнению Шредингера  ,
, .
. .
. , не может находиться более двух электронов с разной ориентацией спинов. Удовлетворяющая этому условию полная волновая функция системы должна быть антисимметричной, то есть менять знак при перемене местами двух электронов.
, не может находиться более двух электронов с разной ориентацией спинов. Удовлетворяющая этому условию полная волновая функция системы должна быть антисимметричной, то есть менять знак при перемене местами двух электронов.
 Здесь
Здесь обеспечивает нормировку функции
обеспечивает нормировку функции  .
.
 .
. . (4.5)
. (4.5) - некоторая периодическая функция с периодом, равным периоду решетки, зависящая от волнового вектора
- некоторая периодическая функция с периодом, равным периоду решетки, зависящая от волнового вектора  .
. ,
,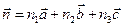 ,
, – векторы единичных трансляций,
– векторы единичных трансляций, - произвольные целые числа.
- произвольные целые числа. , он совмещается сам с собой.
, он совмещается сам с собой. отличается от волновой функции
отличается от волновой функции 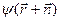 некоторым постоянным множителем
некоторым постоянным множителем . (4.6)
. (4.6) .
. ,
, ,
,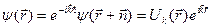 ,
,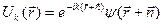 .
.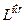 ,
, , определяемая уравнением (4.5), называется функцией Блоха.
, определяемая уравнением (4.5), называется функцией Блоха.