 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Параметрические методы изучения связи
Измерение тесноты (силы) и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака и одного (при изучении парных зависимостей) или нескольких (множественных зависимостей) факторных признаков. Линейный коэффициент корреляции характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости. В теории разработаны и на практике применяются различные модификации формулы расчета данного коэффициента:
Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой:
Линейный коэффициент корреляции изменяется в пределах от -1 до +1: [-1 < r < 1]. Знаки коэффициентов регрессии и корреляции совпадают. Оценка линейного коэффициента корреляции
В случае наличия нелинейной зависимости между двумя признаками для измерения тесноты связи применяют корреляционное отношение. Различают эмпирическое и теоретическое корреляционное отношение. Эмпирическое корреляционное отношение рассчитывается по данным группировки:
где Теоретическое корреляционное отношение определяется по формуле:
где
Корреляционное отношение изменяется в пределах от 0 до 1 [0 < На практике часто приходится исследовать зависимость результативного признака от нескольких факторных признаков. В этом случае статистическая модель может быть представлена уравнением регрессии с несколькими переменными величинами. Такая регрессия называется множественной. Например, линейная регрессия с т независимыми переменными имеет вид:
Множественный коэффициент корреляции вычисляется при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков. Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: 0 < R < 1. Приближение R к единице свидетельствует о сильной зависимости между признаками. Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признаками х1 и х2 при фиксированном значении других факторных признаков, то есть когда влияние х3 исключается, то есть оценивается связь между х1 и х2 в «чистом виде».
Поиск по сайту: |
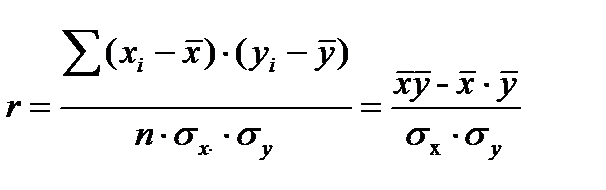


 и
и  — межгрупповая и общая дисперсия результативного признака (y).
— межгрупповая и общая дисперсия результативного признака (y).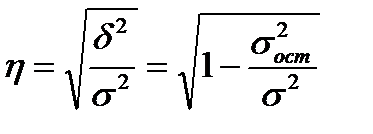
 — остаточная дисперсия.
— остаточная дисперсия. < 1].
< 1].