|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Свойства степенных рядов
10. На промежутке сходимости степенной ряд можно почленно дифференцировать. Интервал сходимости полученного ряда тот же, что и для исходного ряда. 20. На промежутке сходимости степенной ряд можно почленно интегрировать. Интервал сходимости полученного ряда тот же, что и для исходного ряда. 30. Если на интервале функцию можно разложить в степенной ряд, то это разложение единственно. П р и м е р. Найдите интервал сходимости ряда ♦
П р и м е р. Найдите интервал сходимости ряда ♦ Интервал сходимости ряда П р и м е р. Найдите интервал сходимости ряда ♦
П р и м е р. Найдите сумму ♦ Так как Если
Ряд Тейлора Функция Рядом Тейлора для функции
Разложение функций в ряд Маклорена При П р и м е р. Функцию ♦ Вместо формулы Тейлора применим свойства геометрической прогрессии Разложение в ряд элементарных функций
Для функции
Для функции
Аналогично можно получить разложение
Для функции
сходится при
Для функции
П р и м е р. Разложите в ряд Маклорена функцию ♦ Заменяя
П р и м е р. Разложите в ряд по степеням ♦ В равенстве
Кстати, при П р и м е р. Разложите в ряд по степеням ♦ П р и м е р. Найдите сумму ряда ♦ П р и м е р. С точностью до 0,0001 вычислите ♦ Так как
Упражнения Разложите в ряд по степеням
Ряды Фурье В приложениях науки и техники часто приходится иметь дело с явлениями, повторяющимися или воспроизводящимися через определённый промежуток времени. Такие явления описываются периодическими функциями. Функция
ТЕОРЕМА ДИРИХЛЕ.Если функция где коэффициенты В каждой точке разрыва функции Пусть функция т. е. сходится на всей числовой прямой к её периодическому продолжению. Если функция
Если функция
Если функция
где числа
В каждой точке разрыва функции сумма П р и м е р. Разложите в ряд Фурье Функцию ♦ Так как функция нечетная, то
Ряд Фурье на интервале
При П р и м е р. Разложите в ряд Фурье функцию ♦ При
так как функция четная, т. е.
П р и м е р. Разложите в ряд Фурье функцию ♦ На интервале
При
Поиск по сайту: |
 и его сумму
и его сумму 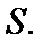
 Если
Если  то ряд расходится, так как общий член стремится к бесконечности, а не к нулю. Поэтому область сходимости ряда
то ряд расходится, так как общий член стремится к бесконечности, а не к нулю. Поэтому область сходимости ряда  Так как
Так как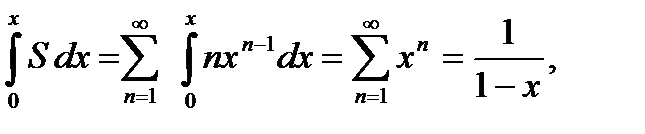 то
то 
 и его сумму
и его сумму 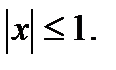 Так как
Так как 
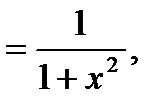 то
то 
 и его сумму
и его сумму Если
Если  то
то 
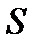 ряда
ряда 
 , то
, то 
 то
то 
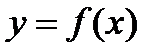 разлагается в степенной ряд на интервале
разлагается в степенной ряд на интервале  , если
, если 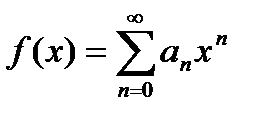 .
.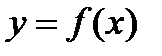 в некоторой окрестности
в некоторой окрестности  точки
точки  называется степенной ряд
называется степенной ряд
 ряд Тейлора называют рядом Маклорена.
ряд Тейлора называют рядом Маклорена.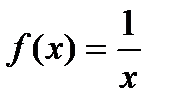 разложите в ряд по степеням
разложите в ряд по степеням 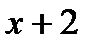 .
. при
при  .
.


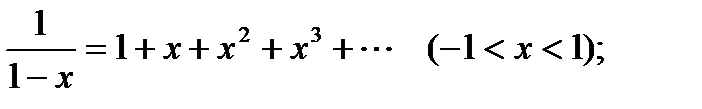


 .
.
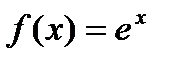 имеем
имеем  Подставив эти значения в формулу ряда Маклорена, получим
Подставив эти значения в формулу ряда Маклорена, получим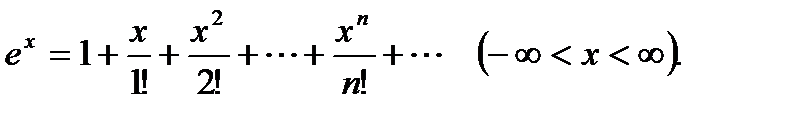
 имеем
имеем 
 Для производных чётного порядка
Для производных чётного порядка  , а нечётного
, а нечётного 
 Подставив эти значения в формулу ряда Маклорена, получим
Подставив эти значения в формулу ряда Маклорена, получим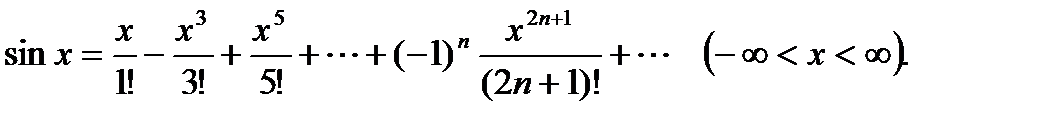

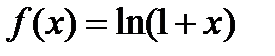 будем исходить из того, что ряд
будем исходить из того, что ряд
 Проинтегрируем обе части равенства
Проинтегрируем обе части равенства
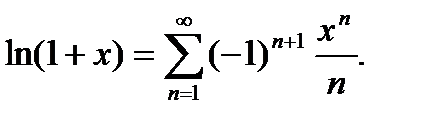
 также применим интегрирование
также применим интегрирование


 на
на  в равенстве
в равенстве  , получим
, получим ;
; 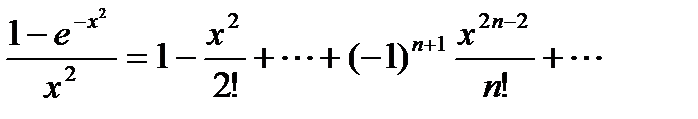 .
.
 , заменяя
, заменяя  ,получим
,получим  . Отсюда
. Отсюда
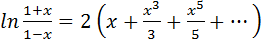 .
.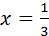 получим
получим  .
. функцию
функцию 

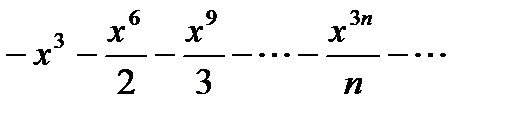 +
+ 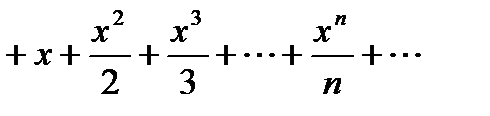


 Следует из разложения в ряд
Следует из разложения в ряд 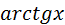

 , то
, то  и
и











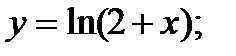



 называется периодической на промежутке Х, если существует число
называется периодической на промежутке Х, если существует число  , для которого из того, что
, для которого из того, что  принадлежат Х следует, что
принадлежат Х следует, что  Период функции наименьшее положительное
Период функции наименьшее положительное  Функции
Функции  периодические с периодом
периодические с периодом  и
и  с периодом
с периодом 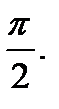 Функция
Функция  удовлетворяет условию Дирихле в интервале
удовлетворяет условию Дирихле в интервале  , если в этом интервале она может иметь конечное число точек разрыва 1-го рода, конечное число точек строгого экстремума и существует положительное число
, если в этом интервале она может иметь конечное число точек разрыва 1-го рода, конечное число точек строгого экстремума и существует положительное число  , для которого
, для которого 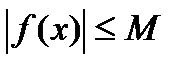 при
при 
 , то во всякой точке
, то во всякой точке 

 вычисляются по формулам
вычисляются по формулам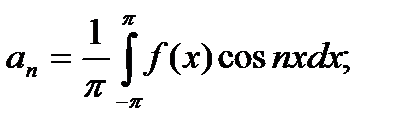

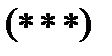
 ряда равна среднему арифметическому
ряда равна среднему арифметическому  пределов слева и справа функции
пределов слева и справа функции  .▄
.▄ Её периодическим продолжением называется функция
Её периодическим продолжением называется функция 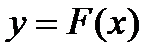 , определённая на всей числовой прямой и периодическая с периодом 2
, определённая на всей числовой прямой и периодическая с периодом 2 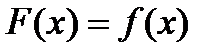 на отрезке
на отрезке  на отрезке
на отрезке  он является периодической функцией с этим же периодом
он является периодической функцией с этим же периодом  чётная, т. е.
чётная, т. е.  , то
, то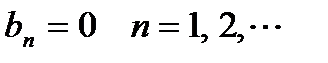

 , то
, то
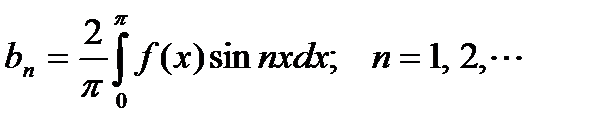
 , то во всякой точке
, то во всякой точке 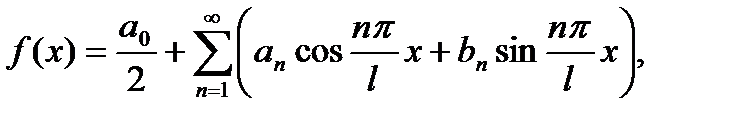
 вычисляются по формулам
вычисляются по формулам

 , а на концах отрезка
, а на концах отрезка 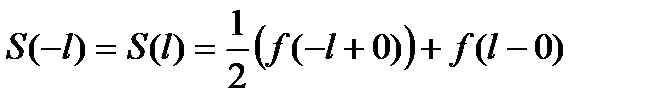 .
.
 а
а
 имеет вид
имеет вид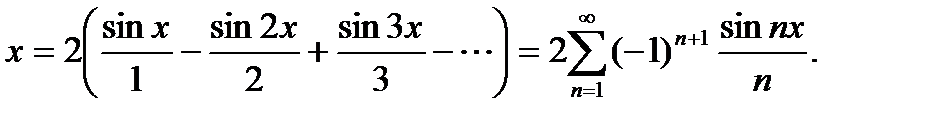
 сумма ряда равна
сумма ряда равна 

 Ряд Фурье на интервале
Ряд Фурье на интервале 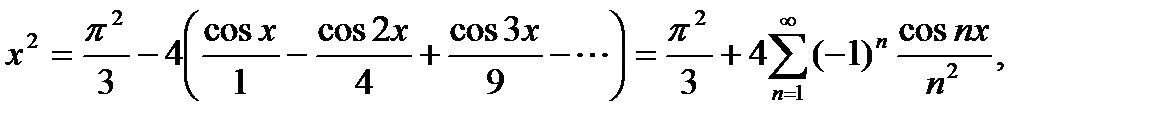

 и
и

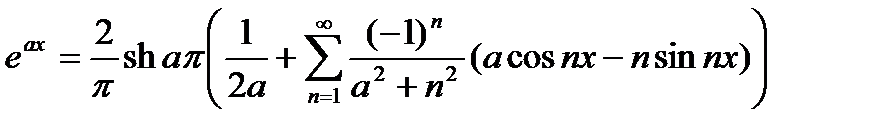 ;
;