 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Свойства сходящихся рядовСтр 1 из 5Следующая ⇒
Дальневосточный федеральный университет Г. К. ПАК РЯДЫ
Владивосток 2011
Глава 10. Ряды Числовые ряды Числовым рядом называется формальная сумма бесконечного количества чисел
Частичными суммами ряда называются суммы первых слагаемых ряда
где П р и м е р. Ряд П р и м е р. Ряд П р и м е р. Ряд П р и м е р. Найдите сумму ряда ♦
Свойства сходящихся рядов
1○. Отбрасывание конечного числа членов ряда не влияет на сходимость или расходимость ряда. 2○. Если ряд сходится и его сумма равна 3○. Если два ряда сходятся и их суммы равны соответственно 4○. Необходимый признак сходимости ряда. Если ряд сходится, то его общий член 5○. Критерий Коши сходимости ряда. Для сходимости ряда необходимо и достаточно, чтобы для любого положительного числа Доказательство свойства 1○. Отбрасывание конечного числа членов ряда изменяет, начиная с некоторого номера, частичные суммы нового ряда на сумму отбрасываемых слагаемых. Для сходящегося исходного ряда по свойствам пределов сумма нового ряда существует; она изменится на эту же сумму отбрасываемых слагаемых. Получился сходящийся ряд. Если после отбрасывания нескольких слагаемых расходящегося ряда он стал сходящимся, то по свойствам пределов сходится и исходный ряд. Противоречие. Доказательство свойства 4○. Если Свойства 2○, 3○ и 5○ докажите самостоятельно. Они следуют из свойств пределов, как и свойства 1о и 4о. П р и м е р. Ряд П р и м е р. Ряд
стремится к бесконечности при
Поиск по сайту: |



 – первая частичная сумма,
– первая частичная сумма,  – вторая частичная сумма, …,
– вторая частичная сумма, …, 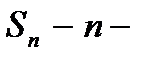 ая частичная сумма. Ряд называется сходящимся, если существует сумма ряда
ая частичная сумма. Ряд называется сходящимся, если существует сумма ряда  – конечный предел последовательности
– конечный предел последовательности  . Ряд называется расходящимся, если этот предел не существует или бесконечен.
. Ряд называется расходящимся, если этот предел не существует или бесконечен. расходится, так как последовательность частичных сумм стремится к бесконечности.
расходится, так как последовательность частичных сумм стремится к бесконечности. расходится, так как не имеет предела последовательность частичных сумм
расходится, так как не имеет предела последовательность частичных сумм  .
. составленный из членов геометрической прогрессии с первым членом
составленный из членов геометрической прогрессии с первым членом  и знаменателем
и знаменателем  , сходится, если
, сходится, если  , и расходится, если
, и расходится, если  Действительно,
Действительно,  и если
и если  при
при  , сумма ряда равна
, сумма ряда равна  . При
. При  предел последовательности частичных сумм бесконечен. Если
предел последовательности частичных сумм бесконечен. Если  то
то  . Если
. Если  то при
то при  чётном
чётном  , а при
, а при  нечётном
нечётном  , т. е. предела частичных сумм нет. Каждый раз, когда
, т. е. предела частичных сумм нет. Каждый раз, когда  ряд расходится.
ряд расходится.
 =
= 
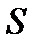 , то сходится и ряд, полученный умножением всех его слагаемых на постоянное число
, то сходится и ряд, полученный умножением всех его слагаемых на постоянное число  , и сумма полученного ряда равна
, и сумма полученного ряда равна 
 и
и  , то и ряд, полученный сложением соответствующих слагаемых этих рядов, тоже сходится и его сумма равна
, то и ряд, полученный сложением соответствующих слагаемых этих рядов, тоже сходится и его сумма равна 
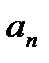 стремится к нулю при
стремится к нулю при 
 нашлось
нашлось  для которого при
для которого при  и любом положительном
и любом положительном  выполняется неравенство
выполняется неравенство
 сумма ряда, то
сумма ряда, то  и
и  , и
, и 
 расходится, так как не выполняется необходимый признак
расходится, так как не выполняется необходимый признак 
 расходится, так как его частичная сумма
расходится, так как его частичная сумма
 Общий член стремится к нулю, а ряд расходится! Признак 4о сходимости ряда не является достаточным.
Общий член стремится к нулю, а ряд расходится! Признак 4о сходимости ряда не является достаточным.