 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Экстремум функции нескольких переменных
Рассмотрим типичную задачу нахождения экстремума функции нескольких переменных, возникающую в экономике. Прибыль от производства разных видов товара
Пусть x1, x2, …, xт. — количества производимых т разновидностей товара, а их цены — соответственно P1, P2, …, Pm (все Pi — постоянные величины). Пусть затраты на производство этих товаров задаются функцией издержек
Тогда функция прибыли имеет вид
Максимум прибыли естественно искать как условие локального экстремума функции многих переменных (8.11) при xi ≥ 0 (при отсутствии других ограничений)
Это условие приводит к системе алгебраических уравнений относительно переменных хi
Система уравнений (8.12) реализует известное правило экономики: предельная стоимость (цена) товара равна предельным издержкам на производство этого товара. Решениями этой системы уравнений являются наборы, состоящие из т значений каждый. Нужно заметить, что сам процесс нахождения решения системы уравнений (8.12) зависит от вида функции издержек и может быть достаточно сложным. Приведем конкретный пример. Пусть производятся два вида товаров, обозначим их количества через x и у. Пусть P1 = 8 и Р2 = 10 — цены на эти товары соответственно, а С = х2 + ху + у2 — функция затрат. Тогда согласно (8.11) при x1 = х, x2 = y прибыль является функцией двух переменных:
Условия локального экстремума приводят к системе линейных алгебраических уравнений
решением которой является точка (2,4). Поскольку
то найденная точка определяет локальный максимум функции прибыли, который равен Пmах = 28.
Оптимальное распределение ресурсов
Рассмотрим типичную задачу оптимального распределения ресурсов на примере функции выпуска и = а0ху2 при допущении, что функция затрат на ресурсы x и у линейна, т.е. имеет вид и = Р1х+Р2у, где P1 и Р2 — соответствующие цены на эти факторы. В точке F(x0, y0), определяющей оптимальное определение ресурсов, линии уровня функций выпуска и затрат касаются (рис. 8.5). Эти линии определяются соответственно уравнениями a0xy2 = C, Р1х + Р2у = А, или у = (b/x)1/2, у = —(Р1/Р2)х + А/Р2, где C > 0 и A > 0 — постоянные числа, b =C/a0. Условие касания этих линий дается уравнением
Из этого уравнения определяется значение x0 = b1/3(P2/2P1)2/3. Тогда из уравнения линии уровня функции выпуска определяется значение у0 = (b/x0)1/2 = b1/3(2P1/P2)1/3. Отсюда получаем, что оптимальное распределение ресурсов х0/у0 должно быть произведено в отношении Р2 : 2P1.
Максимизация прибыли производства продукции
Функция прибыли обычно вычисляется по формуле
где F(K, L) — производственная функция, Р — цена продукции, W и R — соответственно факторные цены на труд и капитальные затраты, L и К — соответственно затраты трудовых ресурсов и капитала. Рассмотрим две задачи, связанные с определением максимума прибыли. 1. Точка (K0, L0) называется оптимальным планом, если в ней функция прибыли (8.13) принимает максимальное значение. Найти предельную норму замещения производственной функции F при оптимальном плане. В точке локального экстремума первые производные функции прибыли П(K, L) равны нулю, откуда имеем систему двух уравнений
Как известно, предельная норма замещения вычисляется по формуле μ = -F'L / F'K, откуда при оптимальном плане получаем μ = -W/R. 2. Максимизация функции прибыли. Найти оптимальный план и максимум функции прибыли (8.13), если F(K, L) = 2(K L)1/3. В данном случае функция прибыли имеет вид
Условия локального экстремума приводят к системе двух линейных алгебраических уравнений относительно координат К0и L0 оптимального плана
Отсюда получаем координаты оптимального плана:
Подстановка этих величин в функцию прибыли дает ее максимум:
Метод наименьших квадратов
Метод наименьших квадратов относится к методам аппроксимации, или приближенного восстановления функции по известным ее значениям в ряде точек. На практике часто возникает задача о наилучшем подборе эмпирических формул, позволяющих представить в аналитической форме данные статистических наблюдений, измерений и т.д. Задача формулируется следующим образом: имеются данные наблюдений в п точках
некоторой величины и и получены соответствующие значения
Нужно подобрать функцию определенного вида и = f(М), чтобы она по возможности наиболее точно отражала общую зависимость измеряемой величины и от параметров (координат) точек измерения {Мi}. Таким образом, задача нахождения эмпирических формул состоит из двух этапов: 1) определение общего вида зависимости f(M) или вида функции f с точностью до постоянных параметров (коэффициентов), входящих в нее; 2) неизвестные коэффициенты подбираются таким образом, чтобы в точках наблюдений (8.14) подобранная функция как можно лучше отвечала данным измерений (8.15). Итак, пусть на первом этапе определено, что эмпирическая формула должна включать совокупность известных базовых функций
т.е. эта формула должна иметь вид
где
— неизвестные параметры эмпирической функции. Второй этап состоит в определении неизвестных параметров (8.18). Их следует выбрать такими, чтобы значения функции (8.17) по возможности наименее всего отклонялись в точках (8.14) от измеренных значений (8.15). Метод наименьших квадратов состоит в минимизации суммы квадратов погрешностей (отклонений) δi (рис. 8.6) функции (8.17) в точках (8.14) как функции от т аргументов — неизвестных параметров:
Для установления точки минимума функции (8.19) т переменных (8.18) нужно найти частные производные этой функции по всем т аргументам и приравнять их к нулю. Отсюда получается система т линейных алгебраических уравнений относительно т неизвестных параметров (8.18)
Коэффициенты и свободные члены уравнений этой системы определяются по формулам
Поскольку функция (8.19) является положительной, выпуклой вниз и неограниченной в евклидовом пространстве Em, то решение системы уравнений (8.20) представляет собой координаты точки ее локального минимума. При обработке данных экономической статистики наиболее распространенным является приближение эмпирической формулой в виде линейной функции одной переменной (например, это широко используется в трендовом анализе). В этом случае совокупность точек измерения (8.14) представляет собой набор значений аргумента x1, х2, ..., xп, а совокупность функций (8.16) состоит из двух функций: x и 1. Эмпирическая формула (8.17) имеет вид
Неизвестные параметры а и b определяются из системы двух линейных уравнений
в которой коэффициенты и свободные члены выражаются формулами
УПРАЖНЕНИЯ
Найти области определения функций.
Построить линии уровня функций.
Найти частные производные от функций.
Найти градиент и его модуль для функций в указанных точках.
8.29. Доказать, что для функций, указанных в задачах 8.23 и 8.24, модуль градиента равен единице во всей области определения.
Найти частные производные второго порядка.
Найти экстремумы функций.
8.43. Найти размеры цилиндра наибольшего объема, если его полная поверхность равна 6π. 8.44. Цены на два вида товаров равны соответственно Р1 = 32 и P2 = 24 денежным единицам. Определить, при каких количествах х и у продаж этих товаров прибыль будет максимальной, если функция издержек имеет вид С = 8.45. В результате эксперимента для пяти значений аргумента x получены пять значений величины и:
Методом наименьших квадратов найти функциональную зависимость между х и и в виде линейной функции и = ах + b.
Поиск по сайту: |


















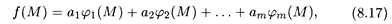







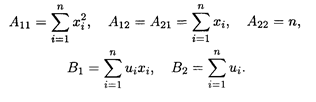







 х2 + 2ху + у2.
х2 + 2ху + у2.