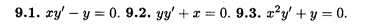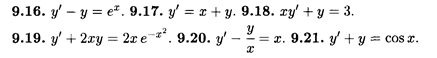|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Линейные уравнения первого порядка
Определение 7.Уравнение вида
где р(х) и q(x) — непрерывные функции, называется линейным дифференциальным уравнением первого порядка. Неизвестная функция и ее производная входят в указанное уравнение в первой степени — линейно, что и объясняет название уравнения. Если q(x) Для линейного уравнения первого порядка можно выписать общее решение с помощью метода вариации постоянной. Здесь это решение приводится без вывода:
Следует отметить, что некоторые нелинейные уравнения приводятся к линейным уравнениям соответствующими заменами неизвестной функции у(х). К таковым относится уравнение Бернулли
где р и q — непрерывные функции, a n — некоторое постоянное число. При п = 0 имеем линейное неоднородное уравнение, а при n = 1 — линейное однородное уравнение
Пусть п ≠ 0, n ≠ 1. Введем новую функцию
тогда
Поделим обе части уравнения (9.9) на уn:
Умножая обе части этого уравнения на (1 — n), с учетом выражений для новой функции z и ее производной получаем линейное дифференциальное неоднородное уравнение относительно неизвестной функции z(x):
В этом уравнении, метод решения которого нам известен, функция z(x) связана с искомой функцией у(x) соотношением (9.10). Рассмотрим примеры решения неоднородных уравнений первого порядка.
Решение. Это линейное неоднородное уравнение первого порядка. Последовательное интегрирование в формуле (9.8) при р(х) = x2 и q(x) = х2 дает
(этот интеграл берется с помощью подстановки t = х3 в формулу (9.8)). Получаем решение дифференциального уравнения:
Решение. Тот же прием, что и в предыдущем примере, при р(х) = 1/х и q(x) = eх дает нам решение
Решение. Данное нелинейное уравнение представляет собой уравнение Бернулли при п = 3. Заменой искомой функции z = у-2, согласно (9.10) и (9.11), получим линейное неоднородное уравнение относительно z(х)
По формуле (9.8) получаем общее решение этого уравнения:
Теперь, выполняя обратную замену у = ±1/
УПРАЖНЕНИЯ
Найти общие решения дифференциальных уравнений методом разделения переменных.
Найти частные решения уравнений первого порядка, удовлетворяющие указанным начальным условиям.
Найти общее решение линейных уравнений.
Решить уравнения Бернулли.
Поиск по сайту: |

 0, то уравнение (9.7) называется линейным однородным уравнением; если же функция q(x) не равна тождественно нулю, то уравнение (9.7) называется линейным неоднородным уравнением.
0, то уравнение (9.7) называется линейным однородным уравнением; если же функция q(x) не равна тождественно нулю, то уравнение (9.7) называется линейным неоднородным уравнением.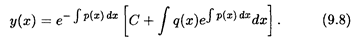



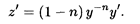










 , получаем решение исходного нелинейного уравнения:
, получаем решение исходного нелинейного уравнения: