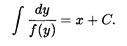|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Уравнения с разделяющимися переменными
Определение 5. Дифференциальное уравнение вида
где f1(x) и f2(y) — непрерывные функции, называется уравнением с разделяющимися переменными. Подчеркнем, что правая часть уравнения представляет собой произведение, в котором один сомножитель зависит только от х, а другой — только от у. Метод решения такого вида уравнений носит название разделения переменных. Запишем производную у' в ее эквивалентной форме как отношение дифференциала функции к дифференциалу независимой переменной
В этом уравнении переменная у входит в левую часть, а переменная х — только в правую, т.е. переменные разделены. Пусть у = φ(x) является решением уравнения (9.3), тогда при подстановке этого решения в уравнение (9.4) получаем тождество: два дифференциала равны друг другу, только в правой части дифференциал выражен через независимую переменную x, а в левой части — через функцию у. Поскольку дифференциалы равны, то их неопределенные интегралы различаются на постоянную величину, т.е., интегрируя слева по переменной у, а справа по переменной х, получаем
где С — произвольная постоянная. Рассмотрим примеры решения уравнений методом разделения переменных. Пример 1. ху' — у = 0, найти частное решение при начальных условиях у0 = 2 при x0 = -4. Решение. Разделим переменные, для чего перенесем у в правую часть, поделим обе части полученного уравнения на ху и умножим их на dx; получим
Интегрируя обе части этого уравнения (правую по x, а левую по у), имеем
где С — произвольная постоянная. При потенцировании получаем
что эквивалентно уравнению у = ±Сх, или у = С1х. Полученная функция представляет семейство интегральных кривых. Для выделения частного решения при указанных начальных условиях подставим в эту формулу х = -4 и у = 2, откуда получим значение для С: С = -1/2. Окончательно частное решение имеет вид
Пример 2. у' = х Решение. Разделяя переменные, получаем уравнение в дифференциалах
Интегрируя, имеем
где С — произвольная постоянная величина. После интегрирования (интеграл в правой части берется при помощи замены переменной) имеем уравнение семейства интегральных кривых
Выделение частного решения, проходящего через точку (0, 1), приводит к определению произвольной постоянной: С =
Неполные уравнения Определение 6. Дифференциальное уравнение первого порядка (9.1) называется неполным, если функция f явно зависит только от одной переменной: либо от х, либо от у. Различают два случая такой зависимости. 1. Пусть функция f зависит только от х. Переписав это уравнение в виде
нетрудно убедиться, что его решением является функция
2. Пусть функция f зависит только от у, т.е. уравнение (9.1) имеет вид
Дифференциальное уравнение такого вида называется автономным. Такие уравнения часто употребимы в практике математического моделирования и исследования природных и физических процессов, когда, например, независимая переменная х играет роль времени, не входящего в соотношения, описывающие законы природы. В этом случае особый интерес представляют так называемые точки равновесия, или стационарные точки,— нули функции f(у), где производная у' = 0. Решение уравнения (9.6) методом разделения переменных приводит к функциональному уравнению для определения неизвестной функции у = φ(x) (или х = ψ(у)):
В общей теории дифференциальных уравнений развита теория качественного анализа, основанная на исследовании характера стационарных точек.
Поиск по сайту: |

 , умножим обе части уравнения (9.3) на dx и поделим обе его части на f2(y), полагая, что f2(у) ≠ 0; получаем
, умножим обе части уравнения (9.3) на dx и поделим обе его части на f2(y), полагая, что f2(у) ≠ 0; получаем





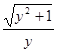 , найти частное решение, проходящее через точку (0,1).
, найти частное решение, проходящее через точку (0,1).


 , т.е. эта кривая описывается уравнением (с учетом выбора знака)
, т.е. эта кривая описывается уравнением (с учетом выбора знака)