Площадь плоской фигуры

Рассмотрим на плоскости Оху фигуру, ограниченную гра­фиком непрерывной и положительной функции f(x) на отрезке [а, b], отрезком [а, b] и вертикальными прямыми х = а и х = b (рис. 7.2). Эту фигуру будем называть криволинейной трапе­цией.

Величина площади криволинейной трапеции равна опреде­ленному интегралу от функции f(x) на отрезке [а, b]:

Если фигура ограничена сверху и снизу неотрицательными функциями f(x) и g(х) соответственно, непрерывными на от­резке [а, b], то площадь S криволинейной фигуры равна разнос­ти площадей криволинейных трапеций, ограниченных сверху графиками f(x) и g(х):

Рассмотрим задачи на вычисление площадей фигур.

Пример 1. Найти площадь фигуры, ограниченной графиком функции у = ln x ≥ 0, осью Ох и прямой х = 2.

Решение. Отрезок интегрирования: 1 ≤ х ≤ 2 (рис. 7.3), так что искомая площадь согласно формуле (7.14) равна:

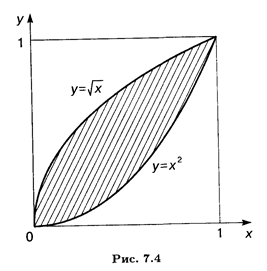
Пример 2. Найти площадь фигуры, ограниченной линиями у = , у = х².

Решение. Вычислим абсциссы точек пересечения указан­ных кривых, для чего приравняем правые части этих уравне­ний: х² = . Корни этого уравнения суть x₁ = 0, x₂ = 1. Сле­довательно, площадь фигуры, ограниченной сверху функцией у = и снизу функцией у = x² (рис. 7.4), дается определенным интегралом на отрезке [0,1]:

Объем тела вращения

Рассмотрим тело, которое образуется при вращении во­круг оси Ох криволинейной трапеции, ограниченной сверху непрерывной и положительной на отрезке [а, b] функцией f(x) (рис. 7.5). Объем этого тела вращения определяется формулой

Если тело образовано вращением криволинейной трапеции вокруг оси Оу, то, выражая х через у как обратную функцию, мы можем получить аналогичным образом формулу для объ­ема тела вращения:

где [c, d] — область изменения функции у = f(x).

Рассмотрим примеры вычисления объемов тел, образован­ных вращением фигур, ограниченных следующими линиями.

Пример 3. у= х², у = вокруг оси Ох.

Решение. Искомый объем вращения равен разности объ­емов, образованных вращением криволинейных трапеций с верхними границами соответственно у = и у = х². Пределы интегрирования определяются по точкам пересечения этих кривых: а = 0 и b = 1. По формуле (7.15) получаем

Пример 4. у = e^х, х = 0, х = 1, у = 0 вокруг оси Оу.

Ррешение. Выражаем х через у: х = ln у; промежуток ин­тегрирования [1, е] определяется очевидным образом. Объем тела вращения (рис. 7.6) равен разности объемов соответствен­но цилиндра радиуса 1 и высоты е и тела вращения вокруг оси Оу криволинейной трапеции, ограниченной сверху кривой х = ln у. Согласно формуле (7.15) получаем

Поиск по сайту: