 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Эксперимент Ш. Кулона с крутильными весами. Закон Кулона.Стр 1 из 9Следующая ⇒
Опыт Перрена по определению масс молекул. Распределение Больцмана и теория броуновского движения Эйнштейна
Опыты Жана Батиста Перрена (1870–1942) окончательно замкнули серию исследований броуновского движения, начавшихся с самого Роберта Брауна. Как читатель мог узнать из раздела, посвященного истории этих исследований, к началу XX века взгляды на природу броуновского движения претерпели целую эволюцию. Тем не менее, математическая теория этого явления обязана появилась только в начале XX века благодаря работам польского математика Мариана Смолуховского (1872–1917) и физика-теоретика Альберта Эйнштейна (1879–1955) Фактически, Перрен получил основные величины, характеризующие микроскопические масштабы молекулярно-кинетической теории: число Авогадро, постоянную Больцмана и характерные массы молекул. Кроме того, в опыте Перрена было подтверждено распределение Больцмана, а неявно — теория броуновского движения Эйнштейна и уравнение Фоккера–Планка, которые приводили к распределению Больцмана на основе механических (в терминологии Эйнштейна — субстатистических) соображений. Таким образом, благодаря данным теориям и описанному выше эксперименту науки о движении (механика) и о теплоте (термодинамика) были окончательно связаны на микроскопическом уровне.
Електрика Ш. Кулона, Эксперимент Ш. Кулона с крутильными весами. Закон Кулона. Дата:1784 Методы:количественный экспериментальный анализ, использование крутильных весов. Прямота эксперимента:непосредственное измерение. Искусственность изучаемых условий:физическая модель — предельно упрощенный вид реально существующего в окружающем мире электростатического взаимодействия (взаимодействие двух шариков). Исследуемые фундаментальные принципы:линейность электростатического взаимодействия
Действительно, заряд, в отличие от массы, может иметь два разных знака — более того, каждое тело состоит из маленьких частиц, имеющих противоположные заряды — электронов и ядер атомов. Этим объясняется способность тел поляризоваться под действием внешнего электрического поля. Электростатическая поляризация тела состоит в том, что отрицательные заряды внутри тела в среднем сдвигаются относительно положительных; тело при этом, как говорят, приобретает ненулевой электрический дипольный момент. В проводниках заряды могут разделяться на макроскопические расстояния, в диэлектриках же поляризация происходит на масштабах порядка атомных: центр электронной оболочки перестает совпадать с ядром атома. Свойством тел поляризоваться во внешнем электрическом поле объясняется способность заряженных тел притягивать незаряженные, например, незаряженные волосы притягиваются к экрану электронно-лучевой трубки монитора, наэлектризованному электронными ударами. По этой причине измерить напрямую силу кулоновского взаимодействия между двумя заряженными шариками оказывается не такой простой задачей — в реальности шарики будут притягиваться ко всем частям экспериментальной установки. Таким образом, в опыте Кулона одна из основных целей — это минимизировать электростатическое взаимодействие шариков не друг с другом, приблизить эксперимент к модели, которую описывает закон Кулона (два точечных заряда в вакууме). Напомним, что перед Кавендишем стояла совсем другая задача — ему требовалось выделить чрезвычайно слабое гравитационное притяжение на фоне других факторов,имеющих, однако, не гравитационный характер.
Кулон также установил, что по отношению к электростатическому взаимодействию справедлив принцип суперпозиции: сила взаимодействия шарика 1 с набором шариков 2…n равна векторной сумме сил взаимодействия его с каждым из этих шариков, описывающихся законом Кулона. Этот факт в современной физике крайне важен и связан с линейностью электромагнитного поля при заданных внешних зарядах и токах. Необходимо отметить, что крутильные весы действительно являются прибором для крайне точных измерений малых сил.
Г. Ома, дата: 1827. Методы:количественный анализ, на основе некоторых общих предположений (например, сопротивление проводника пропорционально его длине). Прямота эксперимента:использованы результаты опытов Эрстеда. Искусственность изучаемых условий:естественные условия, приведенные к простым (линейный проводник, постоянный ток). Исследуемые фундаментальные принципы:закон Ома, дрейфовый характер тока в металлах.
Современный вид закона Ома:
где
Более точные опыты Ом провел, когда было открыто явление термоэлектричества. Теперь в качестве источника ЭДС использовалась дифференциальная термопара (см. схему справа), которая представляет из себя два спая проводников из разных металлов A и B, содержащиеся при разных температурах
где
где
Как видим, реально выдаваемое источником в цепь нагрузки напряжение меньше ЭДС источника. Более того, например, у гальванических элементов (в частности, «сухих», не аккумуляторных батарей) в процессе их эксплуатации внутреннее сопротивление увеличивается (батарея, как говорят, «садится»), что приводит к уменьшению напряжения при тех же нагрузках. Несмотря на кажущуюся очевидность закона Ома, он был принят научной общественностью совсем не сразу после открытия. Скептически настроенные ученые считали, что относительная простота закона обманчива и связана с условиями проводимого эксперимента при достаточно скудных средствах измерения электрических величин. Тем не менее, сегодня этот закон проверен в широких пределах изменения входящих в него величин. По сути дела, закон Ома утверждает, что электродвижущая сила, разгоняющая заряды, полностью компенсируется своеобразным трением тока о кристаллическую решетку проводника, так что заряды дрейфуют по проводнику равномерно. Именно такой, дрейфовый характер тока следует из закона Ома. Скорость дрейфа носителей заряда для проводника площадью 1мм2, через который течет ток 10А, имеет порядок нескольких миллиметров в секунду.
Х. Ерстеда, Дата: 1820. Методы:качественное исследование. Прямота эксперимента: прямое наблюдение, соотнесение с известными свойствами постоянных магнитов. Искусственность изучаемых условий:естественные, упрощенные до модельных. Исследуемые фундаментальные принципы:законы магнитостатики.
Эрстед явился первым, кто пробросил мост между электрическими и магнитными явлениями, пока наполовину качественно. В том же 1820 г., когда Эрстед обнаружил магнитное действие тока, Доминик Араго (1786–1853) обнаружил, что проволочная спираль, по которой течет ток, ведет себя как магнит и способна намагничивать железные опилки. Работу Эрстеда продолжил А.-М. Ампер, который изучил взаимодействие двух токов и предложил математическую формулу для такого, магнитостатического взаимодействия.
А.-М. Ампера Дата: 1820. Методы:качественное и количественное исследование. Прямота эксперимента: прямое наблюдение, соотнесение с известными свойствами постоянных магнитов. Искусственность изучаемых условий:естественные, упрощенные до модельных. Исследуемые фундаментальные принципы:законы магнитостатики, молекулярно-токовое происхождение ферромагнетизма.
Подвижный контур abcd, которым в своих опытах Ампер заменил магнитную стрелку Эрстеда, изображен на рисунке справа. Он подвешен на контактах x и y на металлических кронштейнах, к которым подводится ток, и при этом может свободно вращаться относительно вертикальной оси. Изучая взаимодействие токов с постоянными магнитами и друг с другом, Ампер пришел к следующим выводам: i. взаимодействие токов существует только при замкнутых цепях, т.е. когда по обоим контурам течет ток; ii. параллельные проводники притягиваются, если токи в них текут в одну сторону, и отталкиваются, если в противоположные (это, в некотором смысле слова, противоположно электростатическому притяжению разноименных и отталкиванию одноименных зарядов); iii. сила взаимодействия двух длинных параллельных проводников с током пропорциональна силам тока в них и обратно пропорциональна расстоянию между ними; iv. сила магнитного взаимодействия не отличается в воздухе и в пустоте, в то время как сила кулоновского взаимодействия отличается в этих двух случаях. В том, что сила притяжения длинных параллельных проводников с током обратно пропорциональна расстоянию между ними, Ампер убедился экспериментально с помощью установки, изображенной на рисунке справа. Это, весы, состоящие из неподвижного линейного контура AB с током (см. рис.) и контура CDEF, который может вращаться относительно горизонтальной оси CF. Сила магнитостатического взаимодействия контуров практически полностью определяется взаимодействием линейных проводников AB и DE, поскольку расстояние между ними очень мало. Сила Ампера уравновешивается противовесом W, укрепленным на кронштейне X; кроме того, железная пластинка P на другом конце этого кронштейна фиксирована между двумя постоянными магнитами M. Если вначале, при отключенном токе, уравновесить подвижный контур в положении, в котором его часть DE будет находиться чуть выше AB(как и показано на рисунке), то после включения тока в нужном направлении сила Ампера будет стремиться притянуть проводники друг к другу. Теперь по углу отклонения подвижного контура, определяемому при помощи зеркальца M, можно вычислить величину силы Ампера. С помощью данного прибора Ампер получил свою формулу для силы взаимодействия контуров в виде:
где
Важность открытий Ампера также отмечена в определении единицы измерения силы тока, названной в его честь: «1Ампер — это сила неизменяющегося тока, который при прохождении по двум параллельным проводникам бесконечной длины и ничтожно малой площади поперечного сечения, расположенным в вакууме на расстоянии 1м один от другого, вызвал бы на каждом участке проводника длиной 1м силу взаимодействия, равную
М. Фарадея. Опыты Фарадея и Генри по электромагнитной индукции. Дата: 1831. Методы:качественное и количественное исследование. Прямота эксперимента: прямое наблюдение, в качестве измерительного прибора — гальванометр. Искусственность изучаемых условий:естественные, упрощенные до модельных. Исследуемые фундаментальные принципы:электромагнитная индукция.
Первые опыты, нацеленные на обнаружение такого явления, проводил как сам Майкл Фарадей (1791–1867), так и другие физики, например, Д. Колладон, — однако они не дали положительного результата. Изначально Фарадей предполагал, что ток, будучи жидкостью, протекая в одном проводнике, должен вызывать протекание тока в другой замкнутой цепи, расположенной недалеко от первой. Однако использование неподвижных друг относительно друга проводников и постоянного тока не позволяло обнаружить явление электромагнитной индукции.
Генри за несколько лет до Фарадея поставил опыт, схема которого изображена на рисунке справа, однако он не осознал важности сделанного открытия, не сообщил никому о полученных результатах и не опубликовал их. Генри писал, что обнаружил способ усиления подъемной силы электромагнита до тонны, состоявший в использовании катушек с большим числом витков провода. Но с помощью своего изобретения он также открыл явления самоиндукции и взаимной индукции. Тем не менее, считается, что Генри первым открыл явление самоиндукции: если подключить катушку индуктивности с большим числом витков к источнику напряжения, то ток в катушке будет возрастать постепенно, достигая своего максимального значения, причем тем медленнее, чем больше витков в катушке. Как мы сегодня знаем, в катушке возникает ЭДС самоиндукции, которая препятствует быстрым изменениям тока в ней:
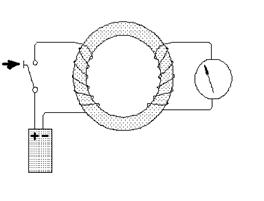
Фарадей же понял, что усиление магнитного потока, производимое катушкой Генри, может помочь в наблюдении искомой электромагнитной индукции, и он независимо от него создал прибор для ее обнаружения. Как уже говорилось, в 1831 г. первый опыт Фарадея показал, что индукционный ток возникает при замыкании и размыкании цепи, намотав двести футов медной проволоки на деревянный барабан и столько же футов вторичной обмотки поверх первой. Однако наблюдаемый эффект был очень слабым. Тогда Фарадей использовал железный кольцевой сердечник (использование железа для усиления действия электромагнитов было тоже предложено Генри), на который наматывал обе обмотки (схема эксперимента изображена выше справа). В результате эффект стал в десятки раз выразительней. Наконец, Фарадей повторил опыт Генри, наблюдая возникновение индукционного тока в катушке при вдвигании и выдвигании из нее другой катушки, в которой тек постоянный ток. Также Фарадей использовал постоянный магнит в качестве второй катушки (см. рис. справа), еще раз убедительно доказав единство электрических и магнитных явлений.
Фарадей всесторонне исследовал явление электромагнитной индукции и предложил ее закон в известной сегодня форме
Поиск по сайту: |
 Мариан Смолуховский
Мариан Смолуховский
 Альберт Эйнштейн
Альберт Эйнштейн
 Жан Батист Перрен
Жан Батист Перрен
 Как, наверное, знает сегодня любой старшеклассник, закон Кулона внешне выглядит аналогично закону всемирного тяготения: сила взаимодействия двух покоящихся точечных зарядов пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Тем не менее, чтобы установить эту закономерность на опыте, необходимо было придерживаться совсем другой экспериментальной стратегии, нежели в опыте Кавендиша по измерению константы всемирного тяготения (более того, опыт Кавендиша был проведен через 10 лет после опыта Кулона).
Как, наверное, знает сегодня любой старшеклассник, закон Кулона внешне выглядит аналогично закону всемирного тяготения: сила взаимодействия двух покоящихся точечных зарядов пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Тем не менее, чтобы установить эту закономерность на опыте, необходимо было придерживаться совсем другой экспериментальной стратегии, нежели в опыте Кавендиша по измерению константы всемирного тяготения (более того, опыт Кавендиша был проведен через 10 лет после опыта Кулона).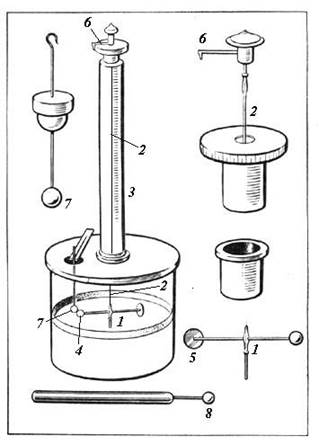 Итак, перейдем к опыту, осуществленному Шарлем Кулоном (1736–1806) в 1784 году (см. рис.). Это изобретенные им крутильные весы, которые через 10 лет использовал в своем опыте Г. Кавендиш. Коромысло 1 было закреплено на шелковой нити 2 в стеклянном сосуде 3, из которого был откачан воздух. На коромысле крепился металлический шарик 4, а на другом конце — противовес 5. Верхний конец нити крепился с помощью специального зажима к стрелке крутильного микрометра 6 (см. схему справа вверху). В сосуд через специальное отверстие можно было помещать второй шарик 7, и тогда из-за взаимодействия шариков нить закручивалась, и силу взаимодействия можно было измерить по повороту стрелки микрометра. Шарики с определенным зарядом Кулон готовил, замыкая два из них через металлическую булавочную головку 8: при этом электрический заряд шариков делился пополам. Это, при достаточной аккуратности, позволяло получать шарики с различным отношением зарядов. С помощью своей установки Ш. Кулон измерял силы до
Итак, перейдем к опыту, осуществленному Шарлем Кулоном (1736–1806) в 1784 году (см. рис.). Это изобретенные им крутильные весы, которые через 10 лет использовал в своем опыте Г. Кавендиш. Коромысло 1 было закреплено на шелковой нити 2 в стеклянном сосуде 3, из которого был откачан воздух. На коромысле крепился металлический шарик 4, а на другом конце — противовес 5. Верхний конец нити крепился с помощью специального зажима к стрелке крутильного микрометра 6 (см. схему справа вверху). В сосуд через специальное отверстие можно было помещать второй шарик 7, и тогда из-за взаимодействия шариков нить закручивалась, и силу взаимодействия можно было измерить по повороту стрелки микрометра. Шарики с определенным зарядом Кулон готовил, замыкая два из них через металлическую булавочную головку 8: при этом электрический заряд шариков делился пополам. Это, при достаточной аккуратности, позволяло получать шарики с различным отношением зарядов. С помощью своей установки Ш. Кулон измерял силы до  Н, при этом убедившись, что сила отталкивания шариков обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна их зарядам
Н, при этом убедившись, что сила отталкивания шариков обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна их зарядам Имя немецкого физика Георга Ома (1787–1854) носит основной закон, описывающий проводимость металлов. Необходимо отметить, что ток, текущий в полупроводниках, сверхпроводниках, электролитах, в вакуумном диоде, не удовлетворяет закону Ома, тем не менее, последний обладает большой общностью, особенно в его дифференциальной форме.
Имя немецкого физика Георга Ома (1787–1854) носит основной закон, описывающий проводимость металлов. Необходимо отметить, что ток, текущий в полупроводниках, сверхпроводниках, электролитах, в вакуумном диоде, не удовлетворяет закону Ома, тем не менее, последний обладает большой общностью, особенно в его дифференциальной форме.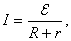
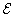 — ЭДС источника питания,
— ЭДС источника питания, 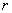 — его внутреннее сопротивление,
— его внутреннее сопротивление, 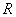 — сопротивление нагрузки, а
— сопротивление нагрузки, а 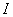 — текущий через нее ток.
— текущий через нее ток. К выражению для своего закона Георг Ом пришел на основании эксперимента, в котором для измерения тока, текущего по проводнику, использовалось открытое Эрстедом и исследованное Ампером магнитное действие тока. Текущий в линейном проводнике ток приводил к повороту крутильных весов, состоявших из магнитной стрелки, подвешенной на упругой нити. Изначально в качестве источника ЭДС Ом использовал вольтов столб из гальванических элементов, однако в силу большого внутреннего сопротивления такого источника экспериментально подтвердить окончательный вид зависимости силы тока от сопротивления нагрузки с его использованием было практически невозможным. Тем не менее, Ом установил правильный вид зависимости, пока что наполовину гипотетически.
К выражению для своего закона Георг Ом пришел на основании эксперимента, в котором для измерения тока, текущего по проводнику, использовалось открытое Эрстедом и исследованное Ампером магнитное действие тока. Текущий в линейном проводнике ток приводил к повороту крутильных весов, состоявших из магнитной стрелки, подвешенной на упругой нити. Изначально в качестве источника ЭДС Ом использовал вольтов столб из гальванических элементов, однако в силу большого внутреннего сопротивления такого источника экспериментально подтвердить окончательный вид зависимости силы тока от сопротивления нагрузки с его использованием было практически невозможным. Тем не менее, Ом установил правильный вид зависимости, пока что наполовину гипотетически.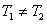 . Такой источник питания обладает малым внутренним сопротивлением, и, кроме того, изменяя разность температур на спаях, можно варьировать его ЭДС. Варьируя длину и материал проводника-нагрузки и ЭДС источника (через изменение температур спаев), Ом пришел к следующей форме своего закона:
. Такой источник питания обладает малым внутренним сопротивлением, и, кроме того, изменяя разность температур на спаях, можно варьировать его ЭДС. Варьируя длину и материал проводника-нагрузки и ЭДС источника (через изменение температур спаев), Ом пришел к следующей форме своего закона: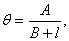
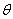 — угол закручивания нити,
— угол закручивания нити,  — длина проводника, а константы
— длина проводника, а константы 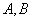 постоянны для данного материала проводника и разности температур спаев. Первую из этих констант Ом называл «электроскопической силой» (впоследствии ЭДС) и установил, что она зависит от разности температур, вторую же он связал с сопротивлением всей цепи, не считая нагрузки. Обобщение полученной экспериментальной формулы и привело к закону Ома, записанному в начале статьи. Также существует так называемый закон Ома для участка цепи, который обычно изучают в школьном курсе физики:
постоянны для данного материала проводника и разности температур спаев. Первую из этих констант Ом называл «электроскопической силой» (впоследствии ЭДС) и установил, что она зависит от разности температур, вторую же он связал с сопротивлением всей цепи, не считая нагрузки. Обобщение полученной экспериментальной формулы и привело к закону Ома, записанному в начале статьи. Также существует так называемый закон Ома для участка цепи, который обычно изучают в школьном курсе физики: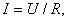
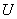 — напряжение (разность потенциалов) на участке цепи,
— напряжение (разность потенциалов) на участке цепи, 
 Ханс Кристиан Эрстед (1777–1851) был, пожалуй, первым, кто стал раскрывать термин «электромагнетизм» в физике, т.е. изучать взаимосвязь электрических и магнитных явлений. Действительно, электростатическое взаимодействие и взаимодействие постоянных магнитов были известны с глубокой древности. Эрстед же в 1820 г. обнаружил, что протекающий по линейному проводнику ток отклоняет магнитную стрелку, находящуюся вблизи него. Если отключить этот проводник от источника питания и расположить по линии север–юг, то стрелка, расположенная рядом с проводником, естественно, будет параллельна ему (см. рис. справа, (а) ). Если же по проводнику пустить ток (см. рис., (б)) , то стрелка повернется на 90 градусов и встанет перпендикулярно ему. Такое же поведение стрелки вызывает приближение ее к постоянному магниту, поэтому естественно сделать вывод, что провод с током также является магнитом, а стрелка выстраивается вдоль его силовых линий.
Ханс Кристиан Эрстед (1777–1851) был, пожалуй, первым, кто стал раскрывать термин «электромагнетизм» в физике, т.е. изучать взаимосвязь электрических и магнитных явлений. Действительно, электростатическое взаимодействие и взаимодействие постоянных магнитов были известны с глубокой древности. Эрстед же в 1820 г. обнаружил, что протекающий по линейному проводнику ток отклоняет магнитную стрелку, находящуюся вблизи него. Если отключить этот проводник от источника питания и расположить по линии север–юг, то стрелка, расположенная рядом с проводником, естественно, будет параллельна ему (см. рис. справа, (а) ). Если же по проводнику пустить ток (см. рис., (б)) , то стрелка повернется на 90 градусов и встанет перпендикулярно ему. Такое же поведение стрелки вызывает приближение ее к постоянному магниту, поэтому естественно сделать вывод, что провод с током также является магнитом, а стрелка выстраивается вдоль его силовых линий.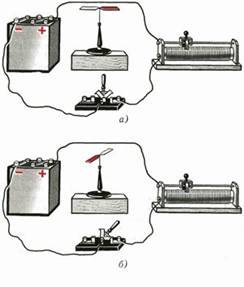 Чтобы подтвердить фундаментальность сделанного открытия, Эрстед использовал проводники из разных металлов, разной толщины и длины, располагал магнитную стрелку под и над проводником с током и на разных расстояниях от него, а также изменял направление и абсолютную величину тока. В итоге он пришел к выводу, что сила магнитного действия тока ослабевает с увеличением расстояния, не зависит от природы проводника (а только от силы тока) и меняет свое направление вместе с изменением направления тока. Также Эрстед отметил, что она имеет «круговой характер» (силовые линии опоясывают проводник). Интересно, что первоначально, заметив отклонение магнитной стрелки из-за текущего тока, Эрстед предположил, что «магнитное действие» излучается проводником с током, как тепловая энергия. Однако дальнейшие исследования показали достаточно нетривиальный характер этого взаимодействия.
Чтобы подтвердить фундаментальность сделанного открытия, Эрстед использовал проводники из разных металлов, разной толщины и длины, располагал магнитную стрелку под и над проводником с током и на разных расстояниях от него, а также изменял направление и абсолютную величину тока. В итоге он пришел к выводу, что сила магнитного действия тока ослабевает с увеличением расстояния, не зависит от природы проводника (а только от силы тока) и меняет свое направление вместе с изменением направления тока. Также Эрстед отметил, что она имеет «круговой характер» (силовые линии опоясывают проводник). Интересно, что первоначально, заметив отклонение магнитной стрелки из-за текущего тока, Эрстед предположил, что «магнитное действие» излучается проводником с током, как тепловая энергия. Однако дальнейшие исследования показали достаточно нетривиальный характер этого взаимодействия. Андре-Мари Ампер (1775–1836) задался вопросом, естественно вытекавшим из исследований Х.К. Эрстеда: если проводник с током отклоняет магнитную стрелку, т.е. ведет себя как магнит, то будет ли он отклонять другой проводник с током? Действительно, магнитная стрелка тоже есть не что иное, как легкий магнит, и ее роль мог бы выполнять легкий и подвижный проводник с током. Между прочим, многие его современники сочли такое обобщение очевидным, когда Ампер заявил о своем открытии — однако, например, железный ключ тоже вызывает отклонение магнитной стрелки, но два таких ключа не притягиваются друг к другу.
Андре-Мари Ампер (1775–1836) задался вопросом, естественно вытекавшим из исследований Х.К. Эрстеда: если проводник с током отклоняет магнитную стрелку, т.е. ведет себя как магнит, то будет ли он отклонять другой проводник с током? Действительно, магнитная стрелка тоже есть не что иное, как легкий магнит, и ее роль мог бы выполнять легкий и подвижный проводник с током. Между прочим, многие его современники сочли такое обобщение очевидным, когда Ампер заявил о своем открытии — однако, например, железный ключ тоже вызывает отклонение магнитной стрелки, но два таких ключа не притягиваются друг к другу.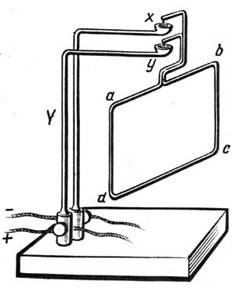 Ампер поставил цель найти количественное выражение для силы взаимодействия элементов тока. Элементом тока
Ампер поставил цель найти количественное выражение для силы взаимодействия элементов тока. Элементом тока 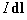 называется малый кусочек
называется малый кусочек 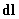 контура из тонкого провода, по которому течет ток
контура из тонкого провода, по которому течет ток 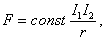
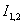 — токи, текущие в проводниках, а
— токи, текущие в проводниках, а 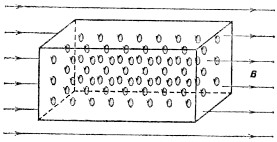 Наконец, необходимо отметить, что исследования привели Ампера к гипотезе о токовой природе постоянных магнитов: в таком магните текут элементарные, молекулярные вихревые токи; он как бы состоит из маленьких контуров с током, и поэтому обладает способностью притягивать опилки, как электромагнит (см. рис.). Это предположение было прорывом во времена Ампера, более того, оно в принципе близко к современному пониманию природы магнетизма. Молекулярные токи Ампера можно ассоциировать с электронами, вращающимися по эллиптическим орбитам атомов. Исследования XX века, однако, показали, что характерный для железа ферромагнетизм (в отличие от диа- и парамагнетизма) имеет место благодаря упорядочению спиновэлектронов, а не плоскостей их орбит. Тем не менее, гипотеза Ампера сохраняет свою важность, хотя бы потому, что почти все другие ученые его времени, включая Био и Лапласа, придерживались противоположной точки зрения: проводник при прохождении через него тока становится магнитом, а не магнит есть совокупность контуров с током.
Наконец, необходимо отметить, что исследования привели Ампера к гипотезе о токовой природе постоянных магнитов: в таком магните текут элементарные, молекулярные вихревые токи; он как бы состоит из маленьких контуров с током, и поэтому обладает способностью притягивать опилки, как электромагнит (см. рис.). Это предположение было прорывом во времена Ампера, более того, оно в принципе близко к современному пониманию природы магнетизма. Молекулярные токи Ампера можно ассоциировать с электронами, вращающимися по эллиптическим орбитам атомов. Исследования XX века, однако, показали, что характерный для железа ферромагнетизм (в отличие от диа- и парамагнетизма) имеет место благодаря упорядочению спиновэлектронов, а не плоскостей их орбит. Тем не менее, гипотеза Ампера сохраняет свою важность, хотя бы потому, что почти все другие ученые его времени, включая Био и Лапласа, придерживались противоположной точки зрения: проводник при прохождении через него тока становится магнитом, а не магнит есть совокупность контуров с током.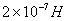 ».
». После открытия Эрстедом и Ампером магнитного действия тока физиков, естественно, стал интересовать вопрос о возможности обратного процесса — создания электрического тока с использованием магнита.
После открытия Эрстедом и Ампером магнитного действия тока физиков, естественно, стал интересовать вопрос о возможности обратного процесса — создания электрического тока с использованием магнита.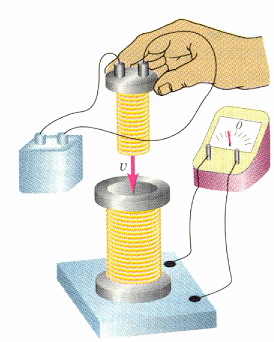 Лишь после шести лет поисков этого явления, в 1831 г., Фарадей сделал предположение о том, что оно должно иметь место при изменении тока, текущего через один из проводников. Более того, он предположил, что в первоначальных его опытах, в которых использовались два параллельных линейных проводника (один, подключенный к источнику питания, другой — к гальванометру) эффект должен был быть очень слабым, хотя и имеющим место в моменты включения и выключения питания. Достигнуть успеха в подтверждении сделанного предположения ему помогла катушка индуктивности, изобретенная Джозефом Генри (1797–1878).
Лишь после шести лет поисков этого явления, в 1831 г., Фарадей сделал предположение о том, что оно должно иметь место при изменении тока, текущего через один из проводников. Более того, он предположил, что в первоначальных его опытах, в которых использовались два параллельных линейных проводника (один, подключенный к источнику питания, другой — к гальванометру) эффект должен был быть очень слабым, хотя и имеющим место в моменты включения и выключения питания. Достигнуть успеха в подтверждении сделанного предположения ему помогла катушка индуктивности, изобретенная Джозефом Генри (1797–1878).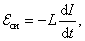
 где
где 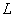 — индуктивность катушки, а
— индуктивность катушки, а 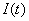 — ток через нее. По сути дела, самоиндукция — это явление влияния на ток в катушке переменного магнитного поля, созданного им самим. Генри также обнаружил явление взаимной индукции, т.е. наведения тока в одной катушке при изменении тока в другой, изолированной от первой. В своем опыте Генри умудрился обнаружить это явление, когда одна катушка располагалась на втором этаже здания, а вторая — в подвале.
— ток через нее. По сути дела, самоиндукция — это явление влияния на ток в катушке переменного магнитного поля, созданного им самим. Генри также обнаружил явление взаимной индукции, т.е. наведения тока в одной катушке при изменении тока в другой, изолированной от первой. В своем опыте Генри умудрился обнаружить это явление, когда одна катушка располагалась на втором этаже здания, а вторая — в подвале.