 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Фінансові ренти (ануїтети) ⇐ ПредыдущаяСтр 3 из 3
Рента - це ціна за використання землі та інших природних ресурсів, пропозиція яких обмежена через їх невідтворюваність.
Економісти-класики на рубежі XVIII ст. поняття ренти зводили лише до ренті земельних ділянок та рудників. Проте сьогодні в різних країнах, в залежності від виду природних ресурсів, виділяють ренту: земельну (у тому числі диференційовану), у добувній промисловості, на будівельні ділянки, монопольну, на людський капітал. Сьогодні визнано, що рента в тій чи іншій мірі присутній в доході будь-якого фактора виробництва (рис.3.3).
Рис. 3.9. Характеристики економічної і чистої економічної ренти Економічною рентою називають платежі власникам факторів виробництва, що перевищують альтернативну вартість цих факторів. Якщо фактор виробництва не має альтернативних варіантів використання, його альтернативна вартість дорівнює нулю, а весь дохід від його застосування виступає у формі ренти. На ринках факторів виробництва земля, її ресурси та нерухомість включені в товарний оборот як ресурси, що не мають альтернатив заміщення в багатьох сферах господарювання. Економічна рента – це наслідок нееластичної чи недостатньо еластичної пропозиції на ринках факторів виробництва. Можна підвищити продуктивність землі, покращити її якість, підвищити ринковий рівень ренти як плати за землю або знизити його до мінімуму, але кількість сукупної пропозиції цього фактора в кожний фіксований момент часу збільшити неможливо. Чиста економічна рента визначається співвідношенням попиту та пропозиції на ринках. Головною особливістю ринку землі є те, що ринковий попит виступає єдиним фактором, що визначає ціну землі або ренту.
Диференціальна земельна рента пов'язана з відмінностями в природній родючості ділянок землі, що обумовлює їх різну граничну продуктивність, а отже, і одержання більш високого доходу при однакових затратах. Ціна землі визначається як дисконтна вартість, розрахована за нескінченний період часу, оскільки земля приносить дохід нескінченно довго:
, де R - розмір щорічної ренти; i - річна процентна ставка.
Ціна землі виступає як капіталізована рента, економічний сенс якої полягає в тому, що вона забезпечує землевласнику таку суму грошей, яка, будучи покладена в банк, приносила би дохід не менший, ніж щорічна рента. Ануїтет (англ. annuity, нім. Annuitat, фр. annuite, з лат. annuitas — щорічний платіж, annus — рік) –це фінансова рента, що становить рівновеликі грошові виплати (чи надходження) через однакові проміжки часу протягом певного періоду.
Рис.3.10. Характеристика фінансової ренти
Ануїтет розглядається як один з видів довготермінової державної позики, за якою щороку виплачують відсотки та погашають частину боргу. Ануїтети були розповсюджені вже в XVII-ХІХ століттях. Відрізняли довічні та строкові ануїтети. Коефіцієнт ануїтету перетворює разову виплату у платіжний ряд. За допомогою цього коефіцієнту визначається періодичність виплат:
i*(1+r) n
I*(1+r) n-1(3.7) де r — відсоткова ставка, n — кількість періодів. Нехай інвестор протягом певного періоду часу в кінці кожного року одержує платежі, які не є однаковими. Якщо він буде інвестувати суму кожного платежу на час до закінчення даного періоду, то після його завершення одержить деяку суму грошей, яку називають майбутньою вартістю потоку платежів. Майбутню вартість потоку платежів можна визначити за формулою:
,
де: F – майбутня вартість потоку платежів; Ct – сума платежу за рік t; r – відсоток, під який інвестується сума платежу розміром Ct; n – кількість років, протягом яких проводяться виплати.
Як видно з формули (3.8), нарахування відсотків на перший платіж здійснюється протягом (n – 1) року, тоді як сама виплата відбувається тільки в кінці першого року.
Часто в практиці фінансового менеджменту виникають ситуації, коли отримують (або виплачують) не одну суму, а декілька, причому виплату (отримання) цих сум проводять за такими правилами: однакова сума через рівні проміжки часу за однієї й тієї самої діючої відсоткової ставки. Такий механізм припливу (відпливу) грошей одержав назву ануїтету або ренти. Теорія ануїтетів є важливою частиною фінансової математики. Вона застосовується при дослідженні проблем доходності цінних паперів, в процесі організації інвестиційного аналізу тощо. Прикладами ануїтету є однакові суми коштів, які перераховують один раз на місяць на депозитний рахунок; однакові суми коштів, які отримують за договором фінансової оренди; однакові щомісячні виплати за кредитом; виплати по облігаціях; премії по страхуванню; регулярні внески до Пенсійного фонду. Зокрема, пенсійний ануїтет – регулярна виплата, яка здійснюється учаснику фонду з накопичувального рахунку (учасника). Деякі фонди надають учасникам вибір отримати їх пенсійні накопичення не щомісячними платежами (чи ануїтетами), а одноразовою виплатою. Розрізняють два основних типи рент: безумовні й умовні ренти. Безумовні – ренти з фіксованим строком, тобто дати першої і останньої виплати визначені до початку ренти. Умовні – ренти, в яких дата першої та останньої виплат залежить від деякої події. Наприклад, пенсія чи премія по страхуванню життя. Рента називається звичайною або постнумерандо, якщо виплати здійснюються в кінці кожного періоду, і приведеною (авансованою, вексельною або пренумерандо), якщо виплати відбуваються на початку кожного періоду. В зв’язку з тим, що період ренти може співпадати або не співпадати з періодом нарахування відсотків, ренти класифікують на прості і загальні.
Найбільший інтерес з практичної точки зору представляють ануїтети, в яких всі платежі рівні між собою (постійні ануїтети) або змінюються у відповідності до деякої закономірності. Як і для простої величини, для ануїтету можна визначити його майбутню та теперішню вартість.
Майбутню вартість ануїтету визначають як суму всіх платежів і складних відсотків, що їх нараховують на кожний платіж за період часу, який пройшов від моменту кожного платежу до моменту останнього платежу. Майбутня вартість ануїтету визначається на момент останнього платежу.
Визначити майбутню вартість звичайного ануїтету можливо за допомогою формули (3.8). Однак її можна привести до більш зручного вигляду, так як величина кожного платежу є однаковою. Помножимо обидві частини рівняння (3.8) на (1 + r) і віднімемо одержаний результат з рівняння (3.8). Одержимо:
або:
або:
Перетворимо формулу (3.11), щоб одержати значення С:
Формулу (3.12) можна використати для практичних фінансових розрахунків ,наприклад, для визначення розміру щорічних відрахувань для формування фонду грошових коштів необхідного розміру, наприклад, пенсійного фонду або фонду по викупу підприємством своїх облігацій.
Майбутня вартість звичайного ануїтету при здійсненні виплат m разів на рік. Якщо умови ануїтету передбачають здійснення платежів m разів на рік, то формула (3.8) набуває вигляду:
де: С – величина виплати за рік.
Помножимо обидві частини рівняння (3.13) на такий вираз:
і потім вирахуємо результат з рівняння (3.13). Після перетворення одержимо:
Тепер розглянемо випадок, який , відрізняється від попереднього тим, що складний відсоток нараховується протягом року m разів, а платежі по ануїтету здійснюються тільки в кінці кожного року. Це означає, що відсотки по першому платежу нараховуються з початку другого року і здійснюються m разів на рік; по другому платежу – з початку третього року і також здійснюються m разів на рік тощо. В даному випадку майбутня вартість ануїтету дорівнює:
Помножимо обидві частини рівняння (3.15 ) на (1 + r/m)m і вирахуємо результат із рівняння (3.16). Після перетворення одержимо:
Приведена вартість ануїтету при нарахуванні відсотку один раз на рік
Оберненим до поняття майбутньої вартості ануїтету є поняття теперішньої вартості ануїтету. Це – теперішня, поточна або сьогоднішня вартість майбутніх рівномірних платежів, які здійснюють через рівні проміжки часу. Теперішня вартість ануїтету розраховується шляхом дисконтування на задану ставку і задану кількість періодів, тобто на величину
або :
де: Р – приведена вартість ануїтету.
Формулу приведеної вартості ануїтету можна також використати у випадку, коли позичальник бере кредит на умовах його погашення в майбутньому щорічними рівними платежами. Для цього знайдемо з формули (3.19) величину С:
де: P – сума кредиту;
r – відсоток по кредиту;
C – платіж по кредиту;
N – термін кредиту.
Приведену вартість ануїтету при здійсненні виплат m разів на рік знаходять дисконтуванням майбутньої вартості ануїтету на (1 + r/m)mn.
Тоді:
Приведена вартість ануїтету при нарахуванні відсотку m разів на рік. Майбутня вартість такого ануїтету розраховується за формулою (3.32). Приведена вартість визначається дисконтуванням правої частини формули (3.21) на (1 + r/m)mn. Тоді отримаємо:
У фінансовому менеджменті особливий інтерес викликає довічна рента, особливо при активізації ринкових відносин в усіх сферах суспільно-економічного життя. Довічна рента –це рента, виплати якої не обмежені ніякими строками. Інша назва довічної ренти – перпетуїтет. Майбутню вартість такого ануїтету визначити неможливо, так як вона не є кінцевою величиною . Однак можна розрахувати приведену вартість довічної ренти, скориставшись формулою (3.19). Оскільки для такого ануїтету n → ∞, то вона набуває вигляду:
Прикладом довічного ануїтету є безстрокові облігації (наприклад, англійська безстрокова державна облігація (консоль), яка випущена у 18 столітті і по ній сплачується дохід кожні півроку) та привілейовані акції, що генерують дохід ( їх власники отримують фіксовані дивіденди, проте не мають права голосу) невизначено тривалий час, тому їх поточна теоретична вартість визначається за формулою (3.23). Найпростішим у розрахунку варіантом оцінки привілейованої акції є відношення величини дивіденду до ринкової норми прибутку за акціями даного класу ризику (наприклад, ставки банківського проценту за депозитами з поправкою на ризик).
Вище було розглянуто звичайний ануїтет, відповідно до якого періодичні та рівномірні платежі здійснюють наприкінці кожного періоду нарахування відсотків. Крім нього існує також авансовий ануїтет (або обернений ануїтет). При авансованому ануїтеті платежі здійснюють не наприкінці кожного періоду нарахування відсотків, а на початку. При цьому кількість платежів однакова, проте періодів нарахування відсотків на один більше порівняно із звичайним ануїтетом. Прикладами приведеної ренти є рахунок в банку, земельна рента, премії по страхуванню.
Для розрахунку майбутньої або теперішньої вартості авансованих ануїтетів можна використати формули розрахунку вартості звичайного ануїтету, трохи переробивши їх шляхом множення відповідної величини на (1 + r). Майбутню вартість ануїтету можна визначити, помноживши формулу (3.23) на (1 + r), так як на кожний платіж відсотки будуть нараховуватися на один рік більше в порівнянні з умовою відкладеного ануїтету.
де: Fn – майбутня вартість негайного ануїтету;
n – кількість років, протягом яких сплачується ануїтет.
Приведену вартість негайного ануїтету знайдемо дисконтуванням правої частини формули (3.24) на (1 + r)n.
або:
де: Pn – приведена вартість негайного ануїтету.
Аналогічно рентам з кінцевим строком довічна приведена рента визначається як послідовність періодичних виплат, що здійснюються на початку кожного періоду нескінченно тривалий час. Приведену вартість негайної довічної ренти можна одержати, помноживши формулу (3.23) на (1 + r). Тоді:
Під поняття рентних платежів в Україні підпадають платежі, що сплачуються за встановленими тарифами, з постачання суб'єктами підприємницької діяльності електричної енергії, а також платежі за природний газ. Зазначені тарифи встановлюються для певних суб'єктів підприємницької діяльності постановами Національної комісії регулювання електроенергетики України. В України на рівні нормативно-правових актів регулюється порядок приймання, транспортування, зберігання, відпуску та обліку нафти і нафтопродуктів на підприємствах і в організаціях України та порядок встановлення нормативів і тарифів на транспортування нафти. Поточні закони про Державний бюджет України регулюють порядок справляння рентної плати та встановлюють процент зарахування рентної плати до централізованого фонду. Для прикладу, суб'єкти підприємницької діяльності, які здійснюють транспортування трубопровідним транспортом територією України природного газу, нафти та аміаку, вносять до Державного бюджету України відповідну рентну плату за транзитне транспортування природного газу і за транспортування нафти магістральними нафтопроводами. Рентні платежі в їх теперішній формі є специфічною формою податку на одиницю продукції, несуть однорідне економічне навантаження і є близькими до акцизу.
Питання для самоперевірки
Поиск по сайту: |






 (3.7)
(3.7)

 К=
К= (3.8 )
(3.8 ) (3.9)
(3.9) (3.10)
(3.10) (3.11)
(3.11) (3.12)
(3.12)

 (3.13)
(3.13) ( 3.14)
( 3.14) (3.15)
(3.15) (3.16)
(3.16) (3.17)
(3.17)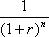 . Отримаємо:
. Отримаємо: (3.18)
(3.18) (3.19),
(3.19),
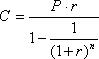 (3.20)
(3.20)
 (3.21)
(3.21) (3.22)
(3.22) (3.23)
(3.23)
 (3.24)
(3.24) (3.25)
(3.25) (3.26)
(3.26) (3.27)
(3.27)