 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Ш.1.2. Потенциал электрического поля
При перемещении единичного заряда q на расстояние dl силами электрического поля совершается работа, определяемая следующим выражением :
На конечном пути L работа равна:
Если электрическое поле создается системой неподвижных зарядов, то работа сил этого поля на пути между произвольными точками зависит только от положения этих точек и не зависит от формы пути. Поля, обладающие таким свойством, называют потенциальными. Очевидно, что при движении заряда по любому замкнутому контуру в таком поле:
Из определения потенциального поля следует, что разность потенциалов между двумя точками электростатического поля dφ равна взятой с обратным знаком работе, совершаемой силой поля при перемещении единичного заряда из одной точки в другую:
Для точек P и P0 достаточно удаленных друг от друга:
причем результат интегрирования не зависит от формы пути. Положение нулевой точки P0 и соответствующего потенциала в ней определяют начало отсчета и в значительной мере произвольны. В частности, в технике часто за нулевой принимают потенциал Земли, в физике – потенциал бесконечно удаленной точки. На практике обычно имеют дело с разностью потенциалов. Введение понятия потенциала позволяет перейти к рассмотрению общих соотношений, описывающих потенциальные поля, в том числе электрическое поле. Из соотношения (1.15) следует, что напряженность поля по направлению l равна по величине и противоположна по направлению производной потенциала по направлению l вектора dl:
т.е. слагающей градиента φ по направлению l:
При этом, если совпадают проекции векторов Eи gradφ, то должны совпадать и сами векторы:
т .е . напряженность электрического поля Eравна градиенту электрического потенциала φ , взятому с отрицательным знаком . Если воспользоваться понятием дивергенции, или расхождения вектора Eкакскалярной величины, определенной в каждой точке поля и являющейся объемной производной этого поля:
где ρ – объемная плотность заряда, создающего поле. В декартовой системе координат выражение (1.20) имеет вид:
Это дифференциальное уравнение связывает дивергенцию вектора электрического поля (плотности источника поля ) в каждой точке поля с величиной объемной плотности заряда в той же точке и является одним из основных уравнений электростатики. Оно позволяет установить связь между плотностью заряда, создающего поле, и разностью потенциалов:
Это уравнение носит название уравнения Лапласа и также является одним из фундаментальных уравнений электростатики. На участках поля, где объемные заряды отсутствуют, т .е . ρ =0, Δφ=0. Уравнение Лапласа позволяет рассчитать распределение потенциала φ и напряженности поля (gradφ), если известно расположение зарядов – источников поля, и обычно используется в тех случаях, когда источниками поля являются металлические электроды, потенциалы которых заданы. В простейших случаях потенциал электрического поля может быть вычислен и непосредственно при определении работы, которую совершает пробный заряд, перемещающийся в поле. Так, можно показать, что для точечного заряда q, поле которого выражается формулой (1.4), его потенциал описывается выражением:
причем значение потенциала при Эквипотенциальные поверхности в таком поле образуют концентрические сферы, потенциал которых описывается выражением (1.24). Отсюда можно сделать вывод, что сфера, имеющая заряд q и радиус a, будет иметь потенциал, значение которого можно вычислить по выражению (1.24) при R=a. При R>a поле, создаваемое такой сферой, не будет отличаться от поля, создаваемого точеным зарядом, находящемся в его центре . Если сферу заменить сплошным металлическим шаром того же радиуса a, товнешнее поле не изменится, потенциал поверхности шара и всего внутреннего объема будет равен φ, а заряд q равномерно распределяется по поверхности шара.
Поиск по сайту: |
 (1.12)
(1.12)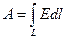 . (1.13)
. (1.13) . (1.14)
. (1.14) . (1.15)
. (1.15) , (1.16)
, (1.16) , (1.17)
, (1.17)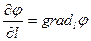 ;
;  (1.18)
(1.18) , (1.19)
, (1.19) , (1.20)
, (1.20) (1.21)
(1.21) . (1.22)
. (1.22) ,(1.24)
,(1.24) равно нулю.
равно нулю.