 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Проверка параметрических гипотез ⇐ ПредыдущаяСтр 2 из 2
1. Проверка гипотез о параметрах распределения.Пусть произведена выборка объема n из нормальной генеральной совокупности, получены выборочные характеристики случайного признака. Рассмотрим нулевую гипотезу Но о том, что генеральная средняя а равна некоторой гипотетической средней ао при альтернативной гипотезе Н1: В первом случае, когда генеральная дисперсия известна, критерием согласия служит нормированная случайная величина
сравнивают с критическим В случае, если генеральная дисперсия неизвестна, для ее оценки используют исправленную выборочную дисперсию
сравнивается с критическим значением Решающее правило: если При альтернативной гипотезе Н1: Проверка гипотезы о равенстве генеральной дисперсии
сравнивают с критическим При альтернативной гипотезе Н1: Предположим теперь, что произведено достаточно большое число n независимых испытаний, в каждом из которых вероятность p появления события постоянна, но неизвестна. Требуется при заданном уровне значимости b проверить нулевую гипотезу Но о том, что неизвестная вероятность р равна некоторой гипотетической вероятности pо при альтернативной гипотезе Н1:
сравнивают с критическим При альтернативной гипотезе Н1:
11.1.Всоответствии с техническими условиями среднее время безотказной работы для приборов из большой партии должно составлять не менее 1000 часов со среднеквадратичным отклонением (СКВО) 100 часов. Выборочная средняя времени безотказной работы для случайно отобранных 25 приборов оказалась равной 970 часам. Считая, что выборочная и генеральная дисперсии совпадают, ответить на вопрос: удовлетворяет ли вся партия техническим условиям, если принять уровень значимости а)b = 0,10; б)b = 0,01? 11.2.Решить задачу 11.1 при условии, что выборочное СКВО составило 11.3.Утверждается, что шарики, изготовленные станком-автоматом, имеют средний диаметр d0= 10 мм. Проверить эту гипотезу, если в выборке из n = 16 шариков средний диаметр оказался равным 10,3мм, считая, что: а) дисперсия известна и равна 11.4.Из большой партии резисторов одного типа и номинала случайным образом отобраны 36 штук. Выборочная средняя величины сопротивления при этом оказалась равной 9,3 кОм. Проверить гипотезу о том, что выборка взята из партии с номиналом 10 кОм, если: а) дисперсия величины сопротивления известна и равна 4 кОм2; б) дисперсия величины сопротивления неизвестна, а выборочная дисперсия равна 6,25 кОм2. Принять b = 0,05. 11.5.По 100 независимым испытаниям найдена относительная частота m/n = 0,14. При уровне значимости 0,05 проверить нулевую гипотезу Но : р = ро = 0,20 при альтернативной гипотезе Н1 : р ¹ 0,20. 11.6.Решить задачу11.5 приальтернативной гипотезе Н1 : р < 0,20. 11.7.Партия изделий принимается, если вероятность того, что изделие окажется бракованным, не превышает 0,03. Среди случайно отобранных 400 изделий оказалось 18 бракованных. Можно ли принять партию? 2. Сравнение дисперсий и средних двух совокупностей.Пусть имеются две независимые выборки малого объема n1 и n2 из двух нормальных генеральных совокупностей, по которым вычислены выборочные средние
Если гипотеза Но верна, то случайная величина Критическое значение tкр.= При альтернативной гипотезе mx ¹ my эмпирическое значение tэмп находят по формуле tэмп =
Если êtэмпç Задача проверки гипотезы о равенстве генеральных дисперсий Эмпирическое значение критерия определяется как отношение выборочных дисперсий Fэмп= (отношение составляется так, чтобы оно было больше единицы). Критическое значение Fкр = Если Fэмп £ Fкр ,то гипотеза H0 принимается, если же Fэмп > Fкр,то гипотеза отвергается. Замечание. Сравнение параметров двух нормальных распределений следует начинать с гипотезы о равенстве дисперсий, и только затем, если она подтвердится, проверить гипотезу о равенстве средних.
11.8. Для сравнения работы двух однотипных измерительных приборов сняты две серии показаний в одних и тех же условиях. Объемы наблюдений n1 = n2 = 15. Получены выборочные средние
¢ Для проверки гипотезы о равенстве дисперсий вычислим эмпирическое значение F – критерия Фишера.
Fэмп=
Найдем табличное (критическое) значение критерия. При уровне значимости Как видно, Fэмп < Fкр , поэтому нет оснований считать, что приборы обладают различной точностью. Вычислим теперь t - критерий для оценки различия средних. Согласно (11.1) получаем:
tэмп= При уровне значимости Так как êtэмп ê< tкр , то различие средних показаний сравниваемых приборов можно считать несущественным. £ 11.9.На двух аналитических весах, в одном и том же порядке взвешены 10 проб химического вещества и получены следующие результаты (в мг):
Установить, значимо ли различие средних и дисперсий результатов взвешиваний, считая, что они распределены нормально. Принять 11.10.При исследовании влияния двух типов покрытия на удельную проводимость телевизионных трубок получены следующие результаты (в условных единицах):
Можно ли на основании этих данных считать, что тип покрытия влияет на удельную проводимость трубок? Принять Вопрос о сравнении нескольких дисперсий
а затем величины
Бартлеттпоказал, что если все дисперсии Если все ni равны между собой, более удобным (и более точным) является критерий Кохрана, показавшего, что случайная величина
имеет распределение, зависящее только от числа выборок m и от числа степеней свободы n, одинакового для всех дисперсий Вернемся к вопросу о сравнении нескольких средних. Предположим, что сравнение дисперсий m выборок показало несущественность различий между ними, т.е. всем выборкам соответствует единая генеральная дисперсия s2. В качестве ее оценки можно взять средневзвешенную дисперсию S2, а для оценки единой генеральной средней а можно взять общую среднюю всех выборок
где ni - объем i-й выборки. В этом случае отношение Если Fэмп
11.11.Проверить гипотезу о равенстве дисперсий по приведённым ниже данным. а) Выборочные дисперсии, вычисленные по результатам трёх серий независимых измерений концентрации : Принять б) Выборочные дисперсии величины контролируемого размера, полученные по результатам выборок из продукции 4-х станков, производящих одни и те же детали:
Принять 11.12.Проверить гипотезу о равенстве дисперсий и средних трех совокупностей, используя следующие результаты наблюдений:
Принять b = 0,05.
Поиск по сайту: |
 Возможны два случая: 1) дисперсия признака в генеральной совокупности известна и равна
Возможны два случая: 1) дисперсия признака в генеральной совокупности известна и равна  ; 2) дисперсия неизвестна.
; 2) дисперсия неизвестна. подчиненная закону
подчиненная закону  Эмпирическое значение критерия
Эмпирическое значение критерия (11.1)
(11.1) при заданном уровне значимости b. Решающее правило: если
при заданном уровне значимости b. Решающее правило: если  то нулевая гипотеза о равенстве выборочной и генеральной средних принимается; если же
то нулевая гипотеза о равенстве выборочной и генеральной средних принимается; если же  нулевую гипотезу следует отвергнуть.
нулевую гипотезу следует отвергнуть. . В качестве критерия используется случайная величина
. В качестве критерия используется случайная величина  распределенная по закону Стьюдента с
распределенная по закону Стьюдента с  степенями свободы. Эмпирическое значение критерия
степенями свободы. Эмпирическое значение критерия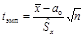 (11.2)
(11.2) при заданном уровне значимости b и числе степеней свободы
при заданном уровне значимости b и числе степеней свободы  гипотеза о равенстве средних принимается; в противном случае гипотеза отвергается.
гипотеза о равенстве средних принимается; в противном случае гипотеза отвергается. правая (левая) граница критической области определяется из равенства
правая (левая) граница критической области определяется из равенства  , а решающим правилом для принятия нулевой гипотезы является условие
, а решающим правилом для принятия нулевой гипотезы является условие 


 при альтернативной гипотезе
при альтернативной гипотезе  осуществляется при помощи критерия
осуществляется при помощи критерия  с числом степеней свободы
с числом степеней свободы  если генеральная средняя известна, и
если генеральная средняя известна, и  если генеральная средняя неизвестна. Эмпирическое значение
если генеральная средняя неизвестна. Эмпирическое значение (11.3)
(11.3)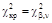 , найденным из таблицы
, найденным из таблицы  нулевая гипотеза принимается. При
нулевая гипотеза принимается. При  гипотезу следует отклонить.
гипотезу следует отклонить. определяют границы двусторонней критической области. Нулевая гипотеза принимается, если эмпирическое значение критерия
определяют границы двусторонней критической области. Нулевая гипотеза принимается, если эмпирическое значение критерия  удовлетворяет условию
удовлетворяет условию  где
где  В противном случае гипотезу отклоняют.
В противном случае гипотезу отклоняют. Известно, что случайная величина
Известно, что случайная величина  распределена асимптотически нормально. Ее эмпирическое значение
распределена асимптотически нормально. Ее эмпирическое значение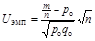 (11.4)
(11.4) найденным в табл. 2 Приложений. При
найденным в табл. 2 Приложений. При  нет оснований отвергнуть нулевую гипотезу; если
нет оснований отвергнуть нулевую гипотезу; если  , нулевая гипотеза должна быть отвергнута.
, нулевая гипотеза должна быть отвергнута.
 правая (левая) граница критической области определяется равенством
правая (левая) граница критической области определяется равенством  а решающим правилом для принятия гипотезы является условие
а решающим правилом для принятия гипотезы является условие 
 В противном случае нулевая гипотеза отвергается.
В противном случае нулевая гипотеза отвергается. часов.
часов. б) оценка дисперсии, определенная по выборке, S2 = = 1,21 мм2. Принять уровень значимости b = 0,05.
б) оценка дисперсии, определенная по выборке, S2 = = 1,21 мм2. Принять уровень значимости b = 0,05. и
и  и исправленные выборочные дисперсии
и исправленные выборочные дисперсии  . Генеральные дисперсии хоть и неизвестны, но считаются равными. Необходимо проверить нулевую гипотезу о том, что mx = my (такие гипотезы о равенстве параметров двух распределений называются простыми). В качестве точечных оценок генеральных средних mx и my можно использовать выборочные средние
. Генеральные дисперсии хоть и неизвестны, но считаются равными. Необходимо проверить нулевую гипотезу о том, что mx = my (такие гипотезы о равенстве параметров двух распределений называются простыми). В качестве точечных оценок генеральных средних mx и my можно использовать выборочные средние 
 распределена нормально с математическим ожиданием
распределена нормально с математическим ожиданием  и дисперсией
и дисперсией  Тогда случайная величина Т =
Тогда случайная величина Т =  подчинена t - распределению Стьюдента с n =
подчинена t - распределению Стьюдента с n =  степенями свободы и служит критерием для оценки нулевой гипотезы о равенстве центров распределения mx = my.
степенями свободы и служит критерием для оценки нулевой гипотезы о равенстве центров распределения mx = my. , соответствующее числу степеней свободы n =
, соответствующее числу степеней свободы n =  и заданному уровню значимости
и заданному уровню значимости  , определяют из табл. 5 Приложений ( t - распределения Стьюдента).
, определяют из табл. 5 Приложений ( t - распределения Стьюдента). где
где  (11.5)
(11.5) , то с надежностью
, то с надежностью  =1-
=1-  сводится к сравнению выборочных дисперсий
сводится к сравнению выборочных дисперсий  и
и 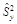 (при альтернативной гипотезе
(при альтернативной гипотезе 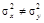 ). Для построения критической области с заданным уровнем значимости
). Для построения критической области с заданным уровнем значимости  или Fэмп =
или Fэмп =  (11.6)
(11.6) определяют по табл. 6 Приложений (таблица F - распределения Фишера) при уровне значимости
определяют по табл. 6 Приложений (таблица F - распределения Фишера) при уровне значимости  = 9,79,
= 9,79,  = 9,60 и выборочные дисперсии
= 9,60 и выборочные дисперсии  = 0,096,
= 0,096,  = = 0,057. Требуется проверить гипотезы о равенстве параметров распределений, т.е. проверить однородность показаний приборов при уровне значимости
= = 0,057. Требуется проверить гипотезы о равенстве параметров распределений, т.е. проверить однородность показаний приборов при уровне значимости  = 0,05.
= 0,05. .
. ;
;




 и средних
и средних  , имеющих числа степеней свободы
, имеющих числа степеней свободы  решается с помощью критерия Бартлетта. Сначала вычисляется средневзвешенная дисперсия
решается с помощью критерия Бартлетта. Сначала вычисляется средневзвешенная дисперсия (11.7)
(11.7) (11.7а)
(11.7а) соответствуют одной генеральной дисперсии, отношение
соответствуют одной генеральной дисперсии, отношение  распределено по закону, близкому к
распределено по закону, близкому к  с числом степеней свободы m - 1 независимо от ni (i = 1,2,...,m), лишь бы все ni были не меньше 5. Значит, гипотеза о равенстве дисперсий принимается, если
с числом степеней свободы m - 1 независимо от ni (i = 1,2,...,m), лишь бы все ni были не меньше 5. Значит, гипотеза о равенстве дисперсий принимается, если  в противном случае различие между дисперсиями
в противном случае различие между дисперсиями  следует считать существенным.
следует считать существенным. (11.8)
(11.8) . Тогда для генеральной дисперсии можно дать следующую оценку:
. Тогда для генеральной дисперсии можно дать следующую оценку: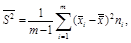 (11.9)
(11.9) имеет F - распределение с числами степеней свободы m - 1 и
имеет F - распределение с числами степеней свободы m - 1 и  . Тогда при уровне значимости
. Тогда при уровне значимости  и сравнить его с эмпирическим Fэмп =
и сравнить его с эмпирическим Fэмп =  .
. ,то справедлива нулевая гипотеза о равенстве вы-борочных средних
,то справедлива нулевая гипотеза о равенстве вы-борочных средних  . В противном случае, когда Fэмп =
. В противном случае, когда Fэмп =  , нулевую гипотезу следует отклонить.
, нулевую гипотезу следует отклонить.





