 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Взаимное расположение прямых в пространстве
Возможны четыре различных случая расположения двух прямых в пространстве: - прямые скрещивающиеся, т.е. не лежат в одной плоскости; - прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку; - прямые параллельные, т.е. лежат в одной плоскости и не пересекаются; - прямые совпадают. Получим признаки этих случаев взаимного расположения прямых, заданных каноническими уравнениями
где
Обозначим через вектор, соединяющий заданные точки. Перечисленным выше случаям взаимного расположения прямых -прямые -прямые --прямые -прямые Эти условия можно записать, используя свойства смешанного и векторного произведений. Напомним, что смешанное произведение векторов в правой прямоугольной системе координат находится по формуле:
Равенство нулю смешанного произведения векторов является необходимым и достаточным условием их компланарности Поэтому: -прямые -прямые -прямые - прямые нальны. Пример 6.Выяснить, лежат ли в одной плоскости прямые
Решение. Прямые лежат в одной плоскости, если их направляющие векторы и вектор, соединяющий точки на этих прямых, компланарны (их смешанное произведение равно нулю). Выпишем из уравнений
Координаты вектора
Поиск по сайту: |

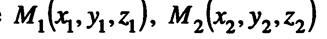 - точки, принадлежащие прямым
- точки, принадлежащие прямым 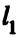 и
и  соответственно, а
соответственно, а 
 - направляющие векторы.
- направляющие векторы.
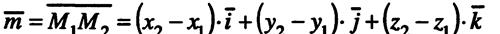
 и
и  соответствуют следующие признаки:
соответствуют следующие признаки: и
и  скрещивающиеся <=>векторы
скрещивающиеся <=>векторы  не
не и
и  пересекаются <=> векторы
пересекаются <=> векторы 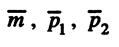 компланарны, а векторы
компланарны, а векторы  не коллинеарны
не коллинеарны и
и  параллельные
параллельные  векторы
векторы  коллинеарны, а
коллинеарны, а не коллинеарны;
не коллинеарны; и
и 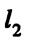 совпадают
совпадают  векторы
векторы  коллинеарны.
коллинеарны.
 и
и  скрещивающиеся
скрещивающиеся  определитель отличен от нуля;
определитель отличен от нуля; и
и  _, пересекаются .
_, пересекаются .  определитель равен нулю, а вторая и третья его строки не пропорциональны, ;
определитель равен нулю, а вторая и третья его строки не пропорциональны, ; и
и  параллельные
параллельные  вторая и третья строки определи
вторая и третья строки определи и
и 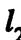 , совпадают
, совпадают  все строки определителя пропорцио-
все строки определителя пропорцио-
 и
и  координаты направляющих векторов
координаты направляющих векторов 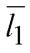 ,
,  и точек
и точек  Прямая
Прямая 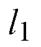 задана параметрически, поэтому координаты
задана параметрически, поэтому координаты  – это коэффициенты при параметре
– это коэффициенты при параметре  а координаты точки
а координаты точки 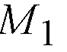 – свободные члены, то есть
– свободные члены, то есть  ={3; 1; –1}, M1(–2; 1; 2). Прямая
={3; 1; –1}, M1(–2; 1; 2). Прямая 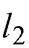 задана канонически, поэтому координаты
задана канонически, поэтому координаты 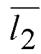 – знаменатели отношений, а координаты точки
– знаменатели отношений, а координаты точки  – свободные члены числителей с минусом, то есть
– свободные члены числителей с минусом, то есть ={2; –1; 1}, M2(1; –1; 0).
={2; –1; 1}, M2(1; –1; 0). есть разности координат
есть разности координат  то есть
то есть (3; –2; –2). Найдем смешанное произведение векторов
(3; –2; –2). Найдем смешанное произведение векторов 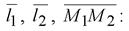
 Смешанное произведение векторов
Смешанное произведение векторов  не ноль, следовательно, эти векторы не компланарны, и прямые не лежат в одной плоскости.
не ноль, следовательно, эти векторы не компланарны, и прямые не лежат в одной плоскости.