 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Уравнение прямой как линии пересечения двух плоскостей
Пусть в координатном пространстве
в которых коэффициенты при неизвестных непропорциональны. Система называется общим уравнением прямой в пространстве.
Замечания.1. Для перехода от общего уравнения прямой к каноническим нужно выполнить следующие действия: 1) найти любое решение
определив тем самым координаты точки 2)найти направляющий вектор нормалей костей:
3) записать канонические уравнения с учетом п.1 и 2. 2.Чтобы перейти от канонических уравнений к общему, достаточно двойные равенства записать в виде системы
и привести подобные члены. 3. Чтобы перейти от канонических уравнений к параметрическим, следует приравнять каждую дробь в уравнениях параметру t и записать полученные равенства в виде системы:
Пример3. Написать канонические и параметрические уравнения прямой, образованной пересечением плоскостей Решение: 1)Найдем координаты фиксированной точки. Из исходной системы уравнений 2) Направляющий вектор определяется как векторное произведение нормалей двух плоскостей, образующих прямую:
3) Запишем канонические уравнения: 4) Обозначив
Пример 4.Составить канонические и общее уравнения прямых, проходящих через точку Решение: а)Пусть прямая
Получим общее уравнение б)Пусть прямая
б) Пусть прямая ских уравнениях прямой означают, что числители тоже равны нулю, то есть у всех точек прямой
Поиск по сайту: |
 _ (в прямоугольной системе координат) две плоскости заданы общими уравнениями
_ (в прямоугольной системе координат) две плоскости заданы общими уравнениями
 пересекаются , поско льку их нормали
пересекаются , поско льку их нормали 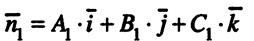 и
и  неколлинеарны. Тогда линия пересечения плоскостей описывается системой уравнений
неколлинеарны. Тогда линия пересечения плоскостей описывается системой уравнений 

 системы
системы
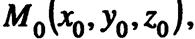 принадлежащей прямой;
принадлежащей прямой; прямой, перпендикулярный к векторам нормалей каждой из плоскостей как векторное роизведение
прямой, перпендикулярный к векторам нормалей каждой из плоскостей как векторное роизведение заданных плос-
заданных плос-



 и
и  .
. исключим
исключим  . Положим
. Положим 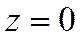 , тогда:
, тогда:  , откуда находим:
, откуда находим:  ,
,  . Таким образом, нашли координаты фиксированной точки
. Таким образом, нашли координаты фиксированной точки 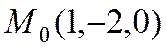 .
. .
. , или
, или  .
. , получаем параметрические уравнения:
, получаем параметрические уравнения: ,
,  ,
,  .
. параллельно: а) вектору
параллельно: а) вектору  ={3; 2; 1} б) вектору
={3; 2; 1} б) вектору  ={0; -1; 3}; в) оси
={0; -1; 3}; в) оси 
 проходит через точку
проходит через точку  параллельно вектору
параллельно вектору  имеют вид:
имеют вид: . Канонические уравнения прямой представляет собой два равенства, запишем их, объединив системой:
. Канонические уравнения прямой представляет собой два равенства, запишем их, объединив системой: Упростим уравнения в этой системе,используя свойства пропорции:
Упростим уравнения в этой системе,используя свойства пропорции:

 Причем,каждое уравнение этой системы задает плоскость, содержащую прямую
Причем,каждое уравнение этой системы задает плоскость, содержащую прямую  .
. проходит через точку
проходит через точку  параллельно вектору
параллельно вектору  ={0; -1; 3} , тогда канонические уравнения
={0; -1; 3} , тогда канонические уравнения 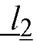 имеют вид:
имеют вид: Ноль в знаменателе канонических уравнений прямой означает, что числитель тоже равен нулю, то есть
Ноль в знаменателе канонических уравнений прямой означает, что числитель тоже равен нулю, то есть  и у всех точек пря мой
и у всех точек пря мой  абсцисса одинакова,
абсцисса одинакова,  . Таким образом, получено уравнение одной плоскости, в которой лежит
. Таким образом, получено уравнение одной плоскости, в которой лежит  . Преобразуем равенство
. Преобразуем равенство  и получим уравнение второй плоскости, содержащей
и получим уравнение второй плоскости, содержащей 
 Общее уравнение
Общее уравнение  :
: 
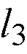 проходит через точку
проходит через точку 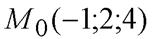 параллельно оси
параллельно оси  , тогда она параллельна орту
, тогда она параллельна орту  то есть
то есть  . Канонические уравнения
. Канонические уравнения  имеют вид :
имеют вид :  Нули знаменателя в канониче-
Нули знаменателя в канониче- :
:  . Плоскость
. Плоскость  – это плоскость, параллельная координатной плоскости
– это плоскость, параллельная координатной плоскости  и отстоящая от нее на 2 единицы, а
и отстоящая от нее на 2 единицы, а  – это плоскость, параллельная координатной плоскости
– это плоскость, параллельная координатной плоскости  и отстоящая от нее на 4 единицы. Таким образом, прямая может быть задана пересечением плоскостей
и отстоящая от нее на 4 единицы. Таким образом, прямая может быть задана пересечением плоскостей  , и общее уравнение
, и общее уравнение  :
: 