 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Измерение напряжения Холла ⇐ ПредыдущаяСтр 4 из 4
1.Включите источник питания электромагнита ИП1. 2.Включите универсальный вольтметр в сеть 220 В. Нажмите на нем клавишу U= , т.е. измерение постоянного напряжения, и клавишу АВП – автоматический выбор предела измерения. 3.Включите источник питания датчика ИП2 и установите с помощью кодового переключателя напряжения ток через миллиамперметр 0,5 мА. 4.Выберите на градуировочном графике электромагнита не менее пяти значений индукции магнитного поля и соответствующие им токи, при которых Вы будете снимать холловское напряжение. Эти значения следует выбрать во всем диапазоне изменения индукции В (а не тока!) через равные интервалы. 5.Установите в цепи электромагнита такой ток, который обеспечит одно из намеченных Вами значений индукции магнитного поля Bn. 6.Снимите зависимость холловского напряжения UH от величины рабочего тока датчика i , изменяя его от 0,5 до 3,0 мА через 0,5 мА. Результаты представьте в виде табл. 2. 7.Повторите измерения п.6 при всех намеченных Вами значениях индукции. Таблица 2
8.Выполнив измерения напряжения Холла, выключите оба источника питания. 9.С помощью универсального вольтметра измерьте электрическое сопротивление датчика r между его токовыми выводами i – i. Для этого нажмите клавишу «R» и клавишу «АВП» – автоматический выбор предела измерения. Указанные выше выводы датчика присоедините к гнездам «R–0». Запишите измеренное сопротивление в табл.2. 10.Занесите в табл.2 сведения о геометрических размерах датчика. Они указаны на панели лабораторной установки. Дополнительное задание. Измерьте напряжение Холла а) при противоположном направлении индукции магнитного поля, б) при противоположном направлении рабочего тока датчика, в) при отсутствии магнитного поля, г)определите направление вектора индукции в зазоре электромагнита. Проанализируйте и дайте объяснение полученным результатам. Обработка результатов измерений.1.Постройте семейство характеристик датчика Холла, т.е. графики зависимости холловского напряжения UH от силы рабочего тока i при всех значениях индукции (график №2). 2.Определите угловой коэффициент К полученных прямых и результаты сведите в табл.3. Таблица 3
3.По данным табл.3 постройте график №3 зависимости углового коэффициента К от индукции В. 4.Из полученного графика №3 определите угловой коэффициент построенной прямой К1. Согласно формуле (4)
5.Определите постоянную Холла RH. Установите ее размерность и единицу измерения. 6.По формуле (5) определите концентрацию носителей тока n в данном образце полупроводникового материала. 7.По электрическому сопротивлению датчика r (упр.2, п.9) и его геометрическим размерам найдите удельную электропроводность s из формулы
8.По формуле (7) определите подвижность носителей тока.
Контрольные вопросы 1. Что такое эффект Холла? Опишите это явление с точки зрения классической электронной теории электропроводности. 2. Какие физические величины можно определить из измерений холловского напряжения? 3. Сравните концентрацию носителей тока, полученную Вами для полупроводника, с концентрацией их в типичных металлических проводниках. Как она зависит от температуры образца? 4. Как устанавливается знак заряда носителей тока из измерений эффекта Холла? Можете ли Вы на основании проведенных измерений определить знак носителей в данном полупроводнике? 5. Что такое подвижность носителей тока? Как она определяется? 6. Объясните, как устроен веберметр. Как им правильно пользоваться? Чем объясняется дрейф стрелки прибора и как это влияет на результаты измерений? Как влияет сопротивление измерительной катушки на результат измерения индукции магнитного поля?
Приложение к лабораторной работе №337 ВЕБЕРМЕТР
В цепь рамки прибора включается наружная изме-рительная катушка с известным числом витков и известной площадью каждого витка. При изменении магнитного потока, пронизывающего измерительную катушку, в ней возникает ЭДС индукции и в цепи рамки флюксметра течет ток, вызы-вающий ее поворот и, следо-вательно, отклонение стрелки прибора. Изменение магнитного потока в катушке можно вызвать различными способами (о них будет сказано ниже). Отклонение стрелки прибора, Рис.4 независимо от ее начального положения, оказывается пропорциональным изменению магнитного потока и может служить для его измерения. Рассмотрим работу веберметра. Запишем уравнение основного закона вращательного движения в проекции на ось вращения
где J – момент инерции подвижной части флюксметра,
M – момент сил, действующих на рамку
где
где I – ток в рамке флюксметра, S – площадь рамки, охваченная по контуру током. Тогда момент силы, вращающей рамку, можно записать так:
Обозначим коэффициент пропорциональности между током и вращающим моментом
Запишем уравнение по второму правилу Кирхгофа с целью определить ток в рамке флюксметра
где ЕК – ЭДС, индуцируемая в измерительной катушке флюксметра при манипуляциях с ней, ЕР – ЭДС, индуцируемая в рамке при повороте ее в магнитном поле флюксметра, R – полное сопротивление цепи прибора (рамки и измерительной катушки). В любом случае ЭДС индукции – это df/dt. Для рамки прибора
где N – число витков в рамке,
Подставляя полученное значение I в уравнение (12), получим
ЭДС индукции в измерительной катушке
Тогда уравнение (14) будет иметь вид
Перепишем его так:
и проинтегрируем
При измерении магнитного поля с помощью флюксметра используется один из трех способов изменения магнитного потока: 1) измерительная катушка поворачивается в измеряемом поле на 90 или 180°; 2) измеряемое магнитное поле выключается или его направление изменяется на противоположное; 3) измерительная катушка переносится из измеряемого поля в область нулевого магнитного поля (полем Земли в этом методе пренебрегают). Во всех трех способах исходное и конечное значение магнитного потока являются константами, скорость изменения потока
Интегрируя уравнение (15) при
При больших t угловая скорость Подставляя
Угол поворота рамки флюксметра Обратим, наконец, внимание на то, что согласно формуле (17) время t, в течение которого затухает движение рамки, должно быть коротким, чтобы приход ее к равновесию был непродолжительным, так как рамка склонна к медленному дрейфу. Самопроизвольное движение стрелки прибора искажает результаты измерений. Из формулы (17) видно, что время установления показаний прибора уменьшается с уменьшением R, поэтому сопротивление измерительной катушки должно быть по возможности малым. Мы хотим с помощью флюксметра измерить индукцию магнитного поля. Такая возможность имеется. Принимая во внимание, что магнитный поток через измерительную катушку в исходном и конечном ее положении принимает следующие значения:
можно написать
где SK и NK – площадь и число витков измерительной катушки, соответственно, f1 и f2 – отсчеты по шкале милливеберметра в исходном и конечном положениях измерительной катушки.
Согласно рекомендации, данной в упр.1, индукцию магнитного поля определим по формуле
где А – постоянная измерительной катушки, ее значение указано на установке.
Список рекомендуемой литературы 1.Савельев И.В. Курс общей физики: Электричество и магнетизм. М.: Наука. 1998. Кн.2. §6.5; 8.3. 2.Сивухин Д.В. Общий курс физики. М.: Наука, 1983. Т.3. §98; 67. 3.Лабораторные занятия по физике /Под ред. Л.Л.Гольдина. М.: Наука, 1983. С.332-342; 281-283.
[1] На рисунках 1 и 2 векторные величины обозначены жирным шрифтом, скалярные – светлым.
Поиск по сайту: |
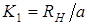 .
.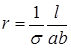 .
.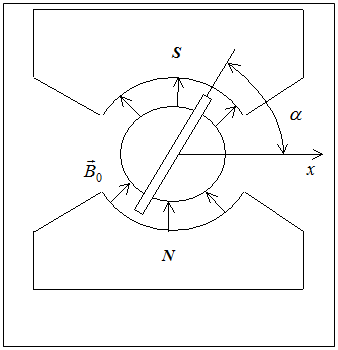 Веберметр (или флюксметр, от англ. flux – поток вектора) предназначен для измерения магнитных потоков. Милливеберметр М119 представляет собой прибор магнитоэлектрической системы (рис.4), который отличается от обычных приборов этой системы тем, что на его рамку не действуют упругие силы, поэтому подвижная система прибора находится в безразличном равновесии [3].
Веберметр (или флюксметр, от англ. flux – поток вектора) предназначен для измерения магнитных потоков. Милливеберметр М119 представляет собой прибор магнитоэлектрической системы (рис.4), который отличается от обычных приборов этой системы тем, что на его рамку не действуют упругие силы, поэтому подвижная система прибора находится в безразличном равновесии [3].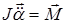 , (8)
, (8)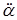 – угловое ускорение,
– угловое ускорение,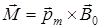 , (9)
, (9)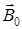 – индукция магнитного поля флюксметра,
– индукция магнитного поля флюксметра,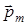 – магнитный момент рамки.
– магнитный момент рамки.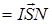 , (10)
, (10)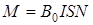 . (11)
. (11)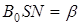 , тогда уравнение (8) можно записать в следующем виде:
, тогда уравнение (8) можно записать в следующем виде: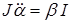 . (12)
. (12) , (13)
, (13)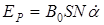 ,
,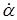 – угловая скорость поворота рамки ( и стрелки) флюксметра
– угловая скорость поворота рамки ( и стрелки) флюксметра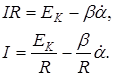
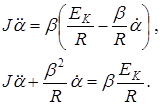 (14)
(14) .
.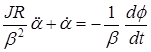 . (15)
. (15)
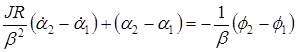 . (16)
. (16)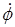 в начале и в конце опыта равна нулю. Кроме того, в начале опыта рамка флюксметра не движется, так что
в начале и в конце опыта равна нулю. Кроме того, в начале опыта рамка флюксметра не движется, так что  . Покажем, что и
. Покажем, что и 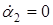 . В самом деле в конце опыта
. В самом деле в конце опыта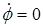 , и в уравнении (15) правая часть обращается в нуль. В отсутствие внешних сил рамка рано или поздно должна остановиться вследствие электромагнитного торможения.
, и в уравнении (15) правая часть обращается в нуль. В отсутствие внешних сил рамка рано или поздно должна остановиться вследствие электромагнитного торможения.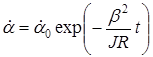 . (17)
. (17)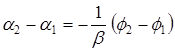 . (18)
. (18)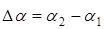 пропорционален изменению магнитного потока, пронизывающего измерительную катушку. Коэффициент пропорциональности 1/b выбран так, что шкала прибора градуируется в милливеберах (в нашем случае).
пропорционален изменению магнитного потока, пронизывающего измерительную катушку. Коэффициент пропорциональности 1/b выбран так, что шкала прибора градуируется в милливеберах (в нашем случае).
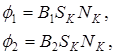
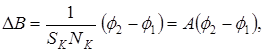 (19)
(19)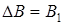 – если выключается ток электромагнита или измерительная катушка удаляется из зазора на значительное расстояние;
– если выключается ток электромагнита или измерительная катушка удаляется из зазора на значительное расстояние;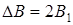 – если переключается направление тока в электромагните или катушка поворачивается внутри зазора на 180°.
– если переключается направление тока в электромагните или катушка поворачивается внутри зазора на 180°.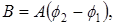 (20)
(20)