 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Выбор оптимальной модели машины
Постановка задачи. На рынке предлагаются три модели машины, отличающиеся производительностью (это – стратегии) и другими параметрами. Предполагаем, что спрос на процессы ремонта объектов с помощью данной машины может быть пониженным (N1=25000, Цп1=50 руб./шт., Требуется выбрать оптимальную модель этой машины по заданному критерию оптимальности с использованием матрицы выигрышей или рисков.
Алгоритм решения: 1. По данным табл. 1 выбираем машину соответствующую заданному производственному участку. Пусть задана тема: «АРМ – мастера тележечного участка». Поэтому в качестве базовой машины выбираем, например, машину для обмывки тележек. 2. Сводим все параметры базовой и проектных моделей моечной машины в таблицу следующей формы «Р» – расчет:
Таблица4.2.1 «Р»
3. Определяем все предусмотренные в таблице параметры машин, учитывая принятые параметры стратегий и ситуаций. Расчеты выполняем с использованием электронной таблицы Excel. Функции, операторы и формулы Excel приведены в теме 2 электронного пособия и в учебном пособии [1]. С этой целью размещаем формат таблицы «Р» в ячейках электронной таблицы. Расчет параметров машины для проектных вариантов осуществляем по соотношениям (5), расчет себестоимости – по формуле (2). 4. Для всех вариантов моделей машины рассчитываем выигрыш по формуле (1). 5. Формируем в электронной таблице матрицу выигрышей по данным таблицы «Р»:
Таблица4.2.2 Матрица выигрышей
6. Определяем итоговый выигрыш для каждой стратегии в зависимости от заданного критерия оптимальности по условиям «О». По заданному критерию выбираем оптимальную модель машины и делаем соответствующий вывод. Строим диаграмму итоговый выигрыш-модель. 7. Для критериев «минимальный средний риск», Сэвиджа строим по матрице выигрышей матрицу рисков и затем проводим процедуру оптимизации.
4.3. Алгоритм расчета и программа. Результаты расчетов. Выводы. Так как я разрабатываю АРМ мастера КРУ, а задание выбор оптимальных моделей машин для депо (ПТО), я выбрал машина для обмывки колесных пар.
Таблица4.3.1 Вариант моего задания.
Вывод: По методу минимальных средних рисков, оптимальный вариант стратегии, Вариант 1.
Поиск по сайту: |
 0,7), средним (N2=37500, Цп2=53 руб./шт.,
0,7), средним (N2=37500, Цп2=53 руб./шт., 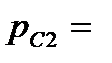 0,9) и повышенным (N3=50000, Цп3=55 руб./шт.,
0,9) и повышенным (N3=50000, Цп3=55 руб./шт.,  0,6) – это ситуации, отличающиеся объемом спроса и вероятностью их появления.
0,6) – это ситуации, отличающиеся объемом спроса и вероятностью их появления. чел
чел
 шт./ч
шт./ч
 шт./ч
шт./ч
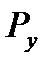 кВт
кВт
 руб.
руб.


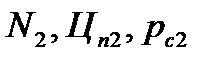

















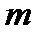 ,*
т.руб./шт.
,*
т.руб./шт.