 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Решения задач с нормальной случайной величиной ⇐ ПредыдущаяСтр 2 из 2
Пример 2. Найти вероятность того, что нормальная СВ с математическим ожиданием 3 и дисперсией 4 примет значение в интервале (-1,5). Решение. По условию
Пример 3. Известно, что масса клубня картофеля определённого сорта является нормально распределённой СВ Х с математическим ожиданием 110 г и средним квадратическим отклонением 30 г. Клубень считается стандартным, если он не повреждён и имеет массу 90-150 г. Определить: 1) процент стандартного картофеля в урожае, если повреждено 10% клубней; 2) величину, которую не превзойдёт масса отдельного клубня с вероятностью 0.95. Решение. 1) По условию Тогда
Это означает, что в урожае имеется 65.68% клубней массой от 90 до 150 г. Так как 90% клубней не повреждено, то процент стандартного картофеля равен 65.68% 2) По условию
Тогда
. Так как Пример 4. Автомат изготавливает шарики для подшипников. Обозначим СВ Х={отклонение фактического диаметра шарика от проектного}. Шарик считается годным, если отклонение диаметра шарика от проектного размера по абсолютной величине меньше 0.7 мм. СВ Х распределена нормально со средним квадратическим отклонением 0.4 мм. Найти число годных шариков среди 100 изготовленных. Решение. По условию
Таким образом, вероятность отклонения, по абсолютной величине меньшего 0.7, равна 0.92. Это означает, что из 100 изготовленных шариков примерно 92 окажутся годными. Пример 5. Станок изготавливает детали. Обозначим СВ Х={фактический размер детали}. Эта СВ распределена по нормальному закону с математическим ожиданием 25 мм (проектный размер) и средним квадратическим отклонением 0.5 мм. Годными считаются детали, размер которых заключён между 23.5 мм и 25.5 мм. Определить: 1) процент бракованных деталей; 2) процент деталей, диаметр которых отклоняется от проектного на величину, не превышающую 0.2 мм. Решение. 1) По условию Воспользуемся формулой Тогда = Это означает, что годные детали составляют 84%, а бракованные – 16%. 2) По условию
Вопросы для самоконтроля знаний
1) Какая случайная величина называется распределённой по биномиальному закону? 2) Какая случайная величина называется распределённой по закону Пуассона? 3) Какая случайная величина называется равномерно распределённой в интервале? 4) Какая случайная величина называется распределённой по нормальному закону? 5) Как определяется вероятность попадания нормально распределённой случайной величины в заданный интервал? 6) Как вычисляется вероятность заданного отклонения нормальной случайной величины от её математического ожидания? 7) Как формулируется правило «трёх сигм»?
Поиск по сайту: |
 . Тогда
. Тогда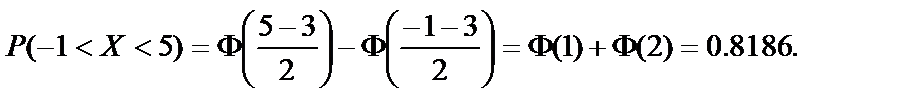
 .
.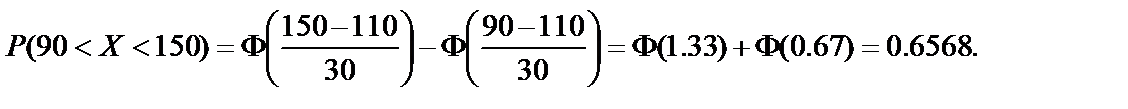
 0.9=59.11%.
0.9=59.11%. . Требуется найти
. Требуется найти 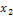 . Применим формулу
. Применим формулу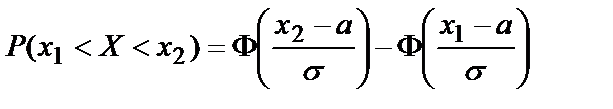 .
.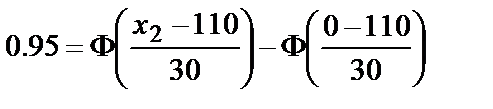 ,
, ,
,  .
. , то
, то 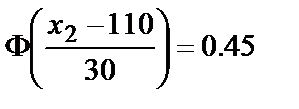 . По таблице найдём
. По таблице найдём 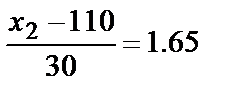 . Отсюда
. Отсюда 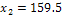 г. Таким образом, можно утверждать, что с вероятностью 0.95 масса отдельного клубня картофеля не превзойдёт 159.5 г.
г. Таким образом, можно утверждать, что с вероятностью 0.95 масса отдельного клубня картофеля не превзойдёт 159.5 г.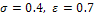 . Воспользуемся формулой
. Воспользуемся формулой 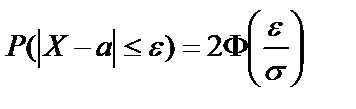 . Так как СВ Х - отклонение, то
. Так как СВ Х - отклонение, то . Тогда
. Тогда 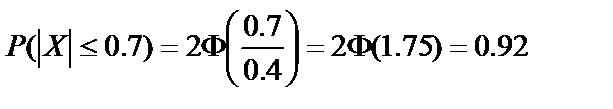 .
.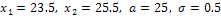 .
.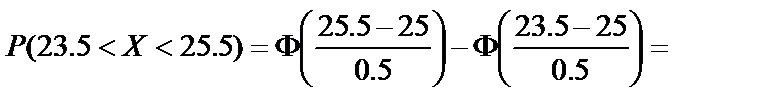
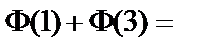
 .
. . В этом случае воспользуемся формулой
. В этом случае воспользуемся формулой  . Тогда
. Тогда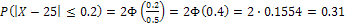 . Это означает, что 31% деталей имеют диаметр, который отклоняется от проектного на величину, не превышающую 0.2 мм.
. Это означает, что 31% деталей имеют диаметр, который отклоняется от проектного на величину, не превышающую 0.2 мм.