 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Нормальный закон распределения и его параметрыСтр 1 из 2Следующая ⇒
Учреждение образования «Белорусская государственная Сельскохозяйственная академия»
Кафедра высшей математики
Методические указания по изучению темы «Основные законы распределения случайной величины» студентами бухгалтерского факультета заочной формы получения образования (НИСПО)
Горки, 2013
Основные законы распределения случайной величины
Биномиальный закон распределения случайной величины
Пусть производится n независимых испытаний, в каждом из которых вероятность наступления некоторого события А одна и та же СВ Х называется распределённой по биномиальному закону, если она может принимать возможные значения X=k с вероятностями, определяемыми по формуле Бернулли
Постоянные величины n и p (q=1-p) называются параметрами биномиального закона распределения. Этот закон распределения можно записать в виде таблицы:
Пример 1. Приживаемость саженцев 90%. В питомнике куплены 4 саженца и посажены на дачном участке. Обозначим СВ Х={количество прижившихся саженцев}. Эта СВ будет распределена по биномиальному закону с параметрами n=4 и p=0.9.
Закон Пуассона
СВ Х называется распределённой по закону Пуассона, если она может принимать возможные значения X=k с вероятностями, определяемыми по формуле Пуассона
Постоянная величина
Математическое ожидание и дисперсия СВ Х, распределённой по закону Пуассона, одинаковы и каждая из этих характеристик равна параметру
Равномерное распределение в интервале
Если все возможные значения СВ содержатся в интервале (a,b) и плотность распределения вероятностей постоянна, то эта СВ называется равномерно распределённой в этом интервале. Из определения такой СВ следует, что
По одному из свойств плотности распределения
График плотности распределения имеет вид:
Функция распределения
График функции распределения имеет вид:
Нормальный закон распределения и его параметры
Пусть плотность распределения вероятностей СВ Х выражается функцией В этом случае говорят, что СВ Х распределена по нормальному закону и её называют нормальной СВ. Нормальный закон распределения играет большую роль в теории и практике. Можно показать, что математическое ожидание нормально распределённой СВ Х равно параметру a, т.е.
Поиск по сайту: |
 , при этом событие А может наступить k раз.
, при этом событие А может наступить k раз.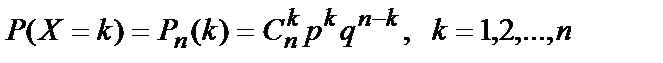 .
.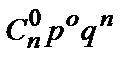
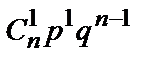
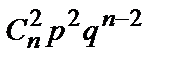

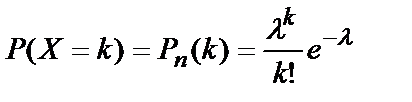 ,
, 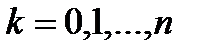 .
.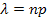 называется параметром этого закона распределения. В этом случае закон распределения СВ Х можно записать в виде таблицы:
называется параметром этого закона распределения. В этом случае закон распределения СВ Х можно записать в виде таблицы: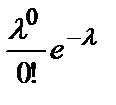
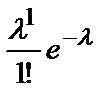
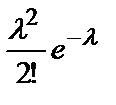

 :
: 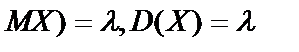 .
.
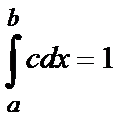 . Тогда
. Тогда 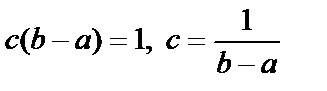 . Следовательно,
. Следовательно,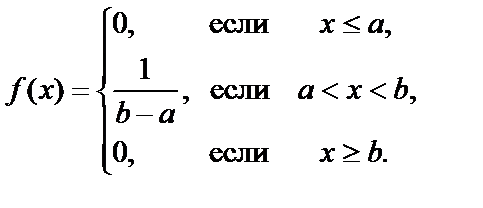
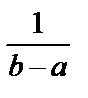
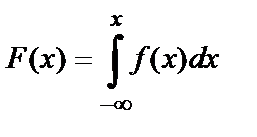 равна
равна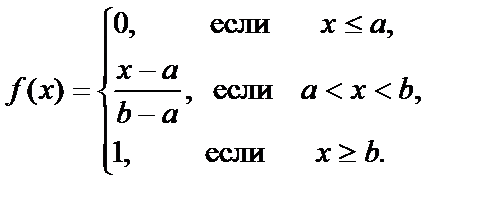
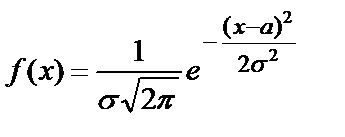 , где а и
, где а и 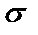 - параметры.
- параметры.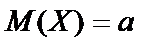 , дисперсия нормальной СВ Х равна
, дисперсия нормальной СВ Х равна 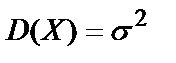 , а
, а 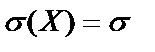 .
.