 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Симплексный метод в задаче линейного программирования.
Задачи линейного программирования могут быть сведены к канонической форме. Введем обозначения: xj - искомые неизвестные, переменные величины (j = 1, …, n) aij - коэффициенты при неизвестных в уравнениях и неравенствах исходных ограничений; vi - величина ограничений в соответствующем уравнении или неравенстве; сj - коэффициенты, с которыми неизвестные входят в целевую функцию;
Формулировка задачи линейного программирования на максимум при n неизвестных определяет функцию цели вида:
F = c1x1+ c2 x2 + … + cj xj + … + cn xn → max;
Если мы имеем дело с канонической формой, то исходящие ограничения bi(i = 1, …, m) задаются m равенствами:
a21x1+ a22 x2 + … + a2j xj + … + a2n xn = b2; ………………………………………………… ai1 x1+ ai2 x2 + … + aij xj + … + ain xn = bi; ………………………………………………… am1x1+ am2 x2 + … + amjxj + … + amnxn = bm Выделяются требования неотрицательности неизвестных xj , т. е.: xj ≥ 0.
Если мы имеем дело с производственно-техническими системами, то ограничения в них обычно принимают форму строгих неравенств, а функция цели может определяться как на максимум, так и на минимум. В этом случае задача линейного программирования в неканонической форме формулируется как:
F = c1x1+ c2 x2 + … + cj xj + … + cn xn → max (min);
a21x1 + a22 x2 + … + a2j xj + … + a2n xn = b2; ……………………………………………………….. ai1 x1 + ai2 x2 + … + aij xj + … + ain xn = bi; ……………………………………………………….. al1 x1 + al2 x2 + … + alj xj + … + aln xn < bl; al+1,1 x1+ al+1,2 x2 + … + al+1,j xj + … + al+1?n xn < bl+1; ………………………………………………………… am1x1 + am2 x2 + … + amjxj + … + amnxn > bm xj ≥ 0
От этой общей формулировки задачи линейного программирования можно перейти к канонической с помощью следующих преобразований. 1. Если в ограничения имеются некоторые bi< 0 , то необходимо все члены соответствующего уравнения (неравенства) умножить на (- 1). 2. Чтобы преобразовать ограничение, записанное в форме неравенства, его превращают в уравнение. Для этого в него добавляется фиктивное неизвестное. При этом стараются в каждое неравенство ограничения ввести собственную фиктивную переменную, знак которого зависит от вида неравенства. Так, в неравенства вида (<) фиктивные переменные вводятся со знаком (+), в неравенства вида (>) – со знаком (-). В результате, после преобразования любой системы неравенств в систему симплексных уравнений, количество неизвестных в системе симплексных уравнений всегда будет больше количества уравнений. Кроме того, при этом образуется единичная подматрица. С помощью этой подматрицы имеется возможность получения в исходной симплексной таблице допустимого решения и проверки ого на оптимальность. Анализ системы (определение ранга матрицы) при больших значениях n может оказаться очень трудоемким. Поэтому целесообразно сразу применять симплексную процедуру, а не отыскивать линейно независимые уравнения. Рассмотрим заполнение симплексной таблицы в общем виде. 1. В первой строке симплексной таблицы записываются показатели критерия оптимальности, т. е. коэффициенты при неизвестных в выражении для целевой функции F. 2. Вторая строка симплексной таблицы называется шапкой матрицы. В ней указываются номера всех неизвестных (основных и фиктивных), входящих в данную систему.
СИМПЛЕКСНАЯ ТАБЛИЦА
3. Далее идут строки, основная часть которых занята коэффициентами при неизвестных в уравнениях исходных условий. Этих строк в матрице должно быть столько, сколько в данной задаче ограничений, или столько, сколько дополнительных неизвестных. 4. Последняя строка носит название целевой строки и заполняется двойственными оценками. Рассмотрим заполнение симплексной таблицы по столбцам: 1. Первый столбец – коэффициенты c j . Он, как и первая строка, отводится для показателей критерия оптимальности. Отличие между первой строкой и первым столбцом состоит в следующем: А) Первая строка, в отличие от столбца, сохраняется лишь в первой симплексной таблице. Начиная со второй итерации, верхняя строка перестает быть обязательной для расчетов. Б) В первой строке указываются все без исключения (основные и дополнительные) показатели критерия оптимальности, т. е. все коэффициенты, с которыми неизвестные входят в целевую функцию. В первый же столбец входит только часть коэффициентов при неизвестных в целевой функции, т. к. число строк в матрице равно числу дополнительных неизвестных. Эта часть состоит из тех показателей, номера которых указаны во втором столбце (p k). 2. Второй столбец - p k. Здесь индекс k соответствует номеру итерации. В этом столбце указываются номера неизвестных, входящих в базисное решение. Эти номера используются для нумерации соответствующих строк матрицы. В первой симплексной таблице (нулевая итерация) в столбце p 0 указываются номера всех дополнительных переменных. 3. Третий столбец - x 0 . В первой симплексной таблице он заполняется свободными членами уравнений из системы ограничений. В процедуре итеративного расчета эти показатели преобразуются в искомое решение, поэтому данный столбец носит название итогового столбца. 4. Значение функции цели - F k . На пересечении итогового столбца и целевой строки помещается значение функционала F k , соответствующее данному этапу решения, т. е. данной итерации k . Это значение равно сумме произведений элементов столбца c j на элементы столбца x 0. 5. Столбцы основания матрицы. Обычно сначала располагаются столбцы для основных неизвестных, вслед за ними – для дополнительных неизвестных. В этих столбцах в первой симплексной таблице приводятся коэффициенты при неизвестных из уравнений исходных условий. 6. Последующие три столбца таблицы: ∑ , α , β имеют вспомогательное значение. Эти столбцы существенно облегчают проведение расчета. Так, в столбце β записываются частные от деления элемента в ключевом столбце и строке i на ключевой элемент. Столбец ∑ используется для проверки хода решения по строкам. Сумма новых элементов должна равняться величине элемента этой строки и столбца ∑ , преобразованного по правилу диагонали. Рассмотрим процедуру на примере решения симплексной задачи, записанной в следующем общем виде:
F = 15 x1+ 20 x2 + 5 x3 → max;
15 x1 + 60 x2 + 0 x3 < 520; 5 x1 + 5 x2 + 90 x3 < 600; xj > 0
Приведем эту задачу к канонической форме. Для этого в каждое из неравенств системы дополнительно введем по одному неизвестному - x4 , x5 , x6. Неравенства превращаются в уравнения:
15 x1 + 60 x2 + 0 x3 + x5 = 520; 5 x1 + 5 x2 + 90 x3 + x6 = 600;
Заполняем первую симплексную таблицу:
Заполненными оказались все клетки таблицы исходя из условий задачи, за исключением последней – целевой - строки. Чтобы заполнить клетку F0 в первой таблице, необходимо просуммировать произведение элементов столбца х0 на элементы столбца с0 , т. е. в данном случае получаем:
F = 600 · 0 + 520 · 0+ 600 · 0 = 0
Чтобы заполнить целевую строку в первой таблице, необходимо для каждого столбца j значение соответствующего коэффициента c j .вычесть из суммы произведений элементов столбца х j на элементы столбца c 0. Таким образом, для столбца х 1 значение величины двойственной оценки равно:
0 · 80 + 0 · 15+ 0 · 5 - 15 = - 15
Соответственно, для столбца х 2 : 0 · 35 + 0 · 60+ 0 · 5 - 20 = - 20 , для столбца х 3 : 0 · 10 + 0 · 0+ 0 · 90 - 5 = - 5 , и т. д. В результате первая симплексная таблица будет иметь вид:
Прежде, чем приступить к решению, необходимо проверить, является ли в предложенной таблице план (решение) оптимальным. Решение считается оптимальным, если все значения чисел в целевой строке положительны. Если полученное решение не является оптимальным, его следует улучшить. Для этого: 1. Выбрать максимальное по абсолютной величине отрицательное значение числа в целевой строке. В данном примере таким числом будет (-20), находящееся в столбце «х 2 ». Именно это значение задает ключевой столбец. Ключевой столбец показывает, какое из неизвестных х j войдет в новое решение задачи. В данном случае в новое решение задачи должно быть включено неизвестное «х 2 ». Для того чтобы включить в новое решение задачи неизвестное х j , улучшающее это решение, необходимо вывести из базисного решения одно из х j , входящих в него. 2. Выбрать минимальное значение частного от деления элементов столбца х0 на элементы ключевого столбца. Результаты этих расчетов заносятся в столбец α симплексной таблицы. В данном случае, поскольку эти отношения равны: 600/35 = 17.14 , 520/60 = 8.67 , 600/5 = 120 , то минимальное значение соответствует х 5 и равно 8.67 . Это отношение задает ключевую строку (рассматриваются только положительные значения α ). 3. Выбрать элемент, находящийся на пересечении ключевого столбца иключевой строки. Этот элемент называется ключевым элементом. В данном случае ключевой элемент находится на пересечении столбца х 2 и строки х 5и равен 60. Ключевым не может быть столбец, все элементы которого оказались отрицательными или нулевыми. 4. Просуммировать элементы матрицы по строкам, начиная от столбца х 0 и кончая столбцом х 6 . Полученные суммы записываются в столбец ∑ . 5. Преобразовать ключевую строку. Для этого: А) каждый элемент ключевой строки делится на ключевой элемент, начиная с элемента столбца х 0 . В данном примере получаем:
Б) в столбце p1 записывается х2вместо х5 ; В) в столбце сj записывается значение критерия оптимальности при х2 , в данном случае 20.
6. Все остальные элементы симплексной таблицы пересчитываются, подчиняясь правилу диагонали, или правилу треугольника:
Для пересчета первого элемента столбца х0 , который данном примере равен 600, необходимо произвести следующие арифметические действия: 600 – 520*35 / 60 = 29б.7 . При пересчете функции цели получим: F = 0 – 520 * (- 20) / 60 ≈ 173. Аналогично рассчитываются все остальные элементы таблицы. В результате получаем новую симплексную таблицу (первая итерация):
Оптимального решения пока что не получено, поскольку не все значения чисел в целевой строке положительны. Произведя достаточное число итераций, можно получить окончательное решение: F = 236.7 ; х1= 3.31 ; х2 = 7.8 ; x3 = 6.05.
Поиск по сайту: |
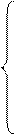 a11x1+ a12 x2 + … + a1j xj + … + a1n xn = b1;
a11x1+ a12 x2 + … + a1j xj + … + a1n xn = b1; a11x1 + a12 x2 + … + a1j xj + … + a1n xn = b1;
a11x1 + a12 x2 + … + a1j xj + … + a1n xn = b1;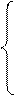 80 x1 + 35 x2 + 10 x3 < 600;
80 x1 + 35 x2 + 10 x3 < 600;
 xj > 0
xj > 0 единичная подматрица_
единичная подматрица_ 1
1
 1
1
