|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
РАСЧЕТ ВАЛА-ШЕСТЕРНИ С ПОМОЩЬЮ СВОБОДНОЙ СЕТКИ КОНЕЧНЫХ ЭЛЕМЕНТОВСтр 1 из 2Следующая ⇒
Федеральное агентство по образованию Государственное образовательное учреждение Высшего профессионального образования «Самарский государственный аэрокосмический Университет имени академика С.П. Королева»
В.Б. Балякин, И.С. Барманов , А.С. Злобин ИСПОЛЬЗОВАНИЕ ПАКЕТА ANSYS ДЛЯ РАСЧЁТА НА ПРОЧНОСТЬ ВЛА - ШЕСТЕРНИ АВИАЦИОННОГО РЕДУКТОРА Утверждено Редакционно-издательским советом университета В качестве методических указаний С А М А Р А Издательство СГАУ
УДК 629.7.03:681.3:65.015.13(06) ББК 39.55 Б 219
Рецензент: д-р техн. наук, проф. Новиков Д.К. Б 219 Балякин В.Б. Использование пакета ANSYS для расчёта на прочность вала - шестерни авиационных редукторов: методические указания / В.Б.Балякин,И.С. Барманов,А.С.Злобин – Самара: Изд-во Самар. гос. аэрокосм. ун-та, 2010. – 20 с.
Рассмотрены концептуальные аспекты проектирования авиационных изделий с помощью ЭВМ. Большое внимание уделено организации моделирования в пакете ANSYS. Рассмотрена возможность применения ANSYS как среды для моделирования при курсовом проектировании на примере вала – шестерни авиационного редуктора.
УДК 629.7.03:681.3:65.015.13(06) ББК 39.55
© Балякин В. Б., Барманов И.С., Злобин А.С., 2010 © Самарский государственный Аэрокосмический университет, 2010
СОДЕРЖАНИЕ Стр. ВВЕДЕНИЕ. 4 1 РАСЧЕТ ВАЛА-ШЕСТЕРНИ С ПОМОЩЬЮ СВОБОДНОЙ СЕТКИ КОНЕЧНЫХ ЭЛЕМЕНТОВ.. 5 2 РАСЧЕТ ВАЛА-ШЕСТЕРНИ С ПОМОЩЬЮ УПОРЯДОЧЕННОЙ СЕТКИ КОНЕЧНЫХ ЭЛЕМЕНТОВ.. 13 ЗАКЛЮЧЕНИЕ. 20
ВВЕДЕНИЕ В данной работе рассматривается методика прочностного расчета деталей машин с помощью метода конечных элементов на примере вала-шестрени авиационного редуктора. Для расчета применяется программный пакет ANSYS (продукт фирмы ANSYS Inc.). Здесь же приведен сравнительный анализ трех путей решения задачи: расчет методами сопротивления материалов, расчет с применением упорядоченной сетки конечных элементов, расчет с применением свободной сетки конечных элементов. Методика решения с помощью свободной сетки приведена из методических указаний «Расчёт на прочность деталей авиационных редукторов с помощью пакета «Ansys»: метод. указание / В.Б.Балякин, А.Г. Кожин, А.Н. Крундаева.
Вал закреплен в радиальном и радиально-упорном подшипниках и приводится во вращение двигателем через шлицевое соединение.
РАСЧЕТ ВАЛА-ШЕСТЕРНИ С ПОМОЩЬЮ СВОБОДНОЙ СЕТКИ КОНЕЧНЫХ ЭЛЕМЕНТОВ
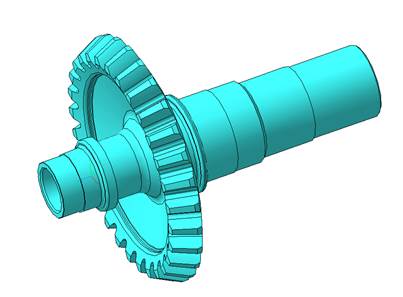
Геометрическая модель шестерни может быть создана в любой программе тpехмеpного моделирования (например КОМПАС-3D V8) см. Рисунок 1.
Рисунок 1 - 3 D модель шестерни
Для расчета на прочность деталь необходимо перевести в программу ANSYS. Для этого создается файл типа parasolid (*.x_t). в КОМПАС-3D V8 (Рисунок 2).
Рисунок 2 - Сохранение 3D модели под расширением *.x_t.
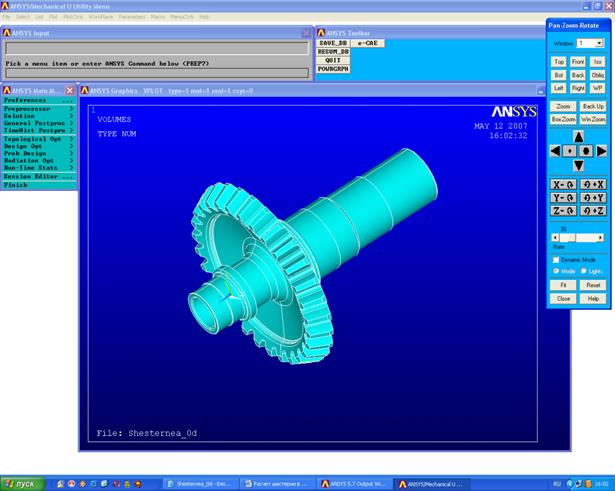
Файл Shesterny_0d.x_t импортируется в ANSYS (File→ Import→PARA…). Рисунок 3.
Рисунок 3 - Перевод шестерни в ANSYS После проделанной операции на экране появится набор линий, но в программу будет перенесено тело с определенным объемом. Для просмотра существования объема необходимо выбрать функцию: List→ Volumes (Рисунок 4).
Рисунок 4 - Результат перевода
Для того чтобы продолжить работу необходимо представить деталь в виде объемного тела PlotCtrls→ Style→Solid Model Facets …. В появившейся вкладке заменяем каркасное изображение объема, на действительное изображение Wireframe→Normal Faceting. Выводим объемное изображение Plot→Volumes. Рисунок 5.
Рисунок 5- Объемное изображение шестерни
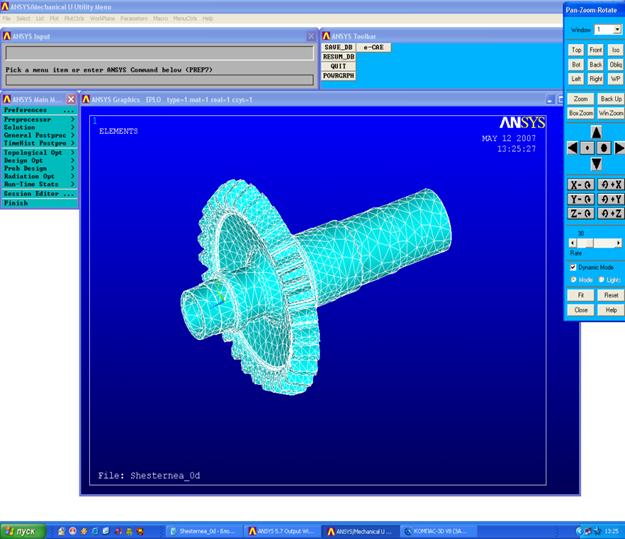
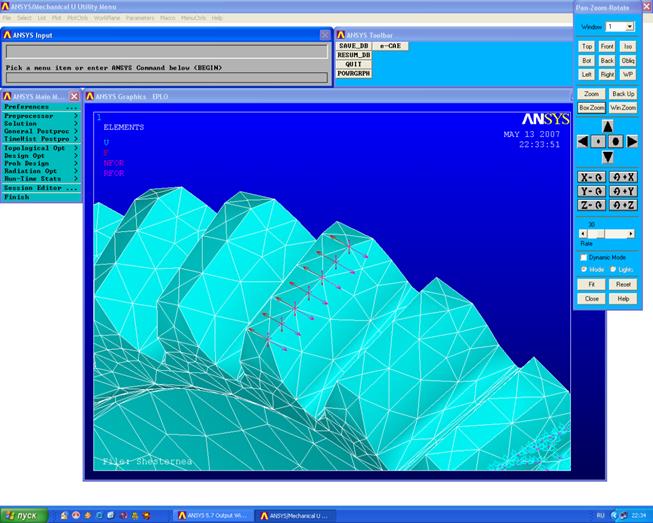
Для разбиения детали на конечные элементы необходимо выбрать тип конечного элемента и задать свойства материала: модуль упругости, коэффициент Пуассона и плотность. Выбор типа конечного элемента Main Menu→Preprocessor→Element Type→Add/ Edit/ Delete→Add. В появившейся вкладке выбираем Solid Tet 10 node 92. Задаём свойства материала Main Menu→Preprocessor→Material Models→Structural→Linear→Elastic→Isotropic. Модуль упругости EX = 2E11 Па; Коэффициент Пуасона MUXY = 0.3; Плотность Density = 7800 кг/м3. Следует пРисуноквоить эти атрибуты шестерне Attributes Define→All Volumes. Воспользуемся функцией разбиения детали на объемные конечные элементы Main Menu→Preprocessor→MeshTool. Нажимаем Set и пРисунокваиваем SIZE Element edge length = 0,007 м. После чего нажимаем mesh и Pick All (см. Рисунок 6).
Рисунок 6- Разбиение шестерни на объемные конечные элементы
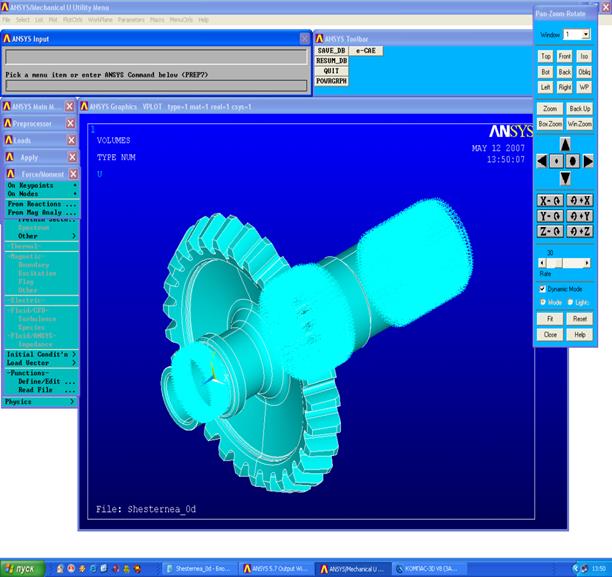
В редукторе шестерня находится в соединении с другими элементами (подшипниками, шайбами, гайками), поэтому необходимо ввести ограничения на перемещение шестерни по осям координат. Перейдем в цилиндрическую систему координат, так как ось шестерни представляет собой систему цилиндров Utility Menu→ WorkPlane→Change Active CS to→ Global Cylindrical. В каждом конечном элементе существует своя система координат, непосредственно связанная с глобальной системой координат. Для правильного приложения нагрузки необходимо изменить положение систем координат узлов так, чтобы они располагались по окружности Main Menu→Preprocessor→ →Modeling/Move/Modify→Rotate Node CS →To Activ CS. Введем ограничения на перемещения в месте расположения шлицов по всем трем осям Main Menu→Preprocessor →Loads→ Apply→Displacement→On Areas. Выделяем интересующую нас поверхность и нажимаем OK. В появившейся вкладке выбираем All DOF. Ограничение необходимо нанести и в те места где расположены подшипники: для радиально упорного ограничиваем по UX и UZ , а радиальный только по UX (см. Рисунок 7).
Рисунок 7- Наложение ограничений
Для правильного приложения нагрузки необходимо перейти в “Декартову” систему координат Utility Menu→WorkPlane→Change Active CS to→Global Cartesian. Рассматриваемое зубчатое колесо имеет наибольшую нагрузку на зубья в момент, когда в зацепление находиться всего одна пара зубьев, так как нагружен всего один зуб. Выбираем поверхность, к которой приложим нагрузку (Select→ Entities). См Рисунок 8.
Рисунок 8- Выбор поверхности нагружения
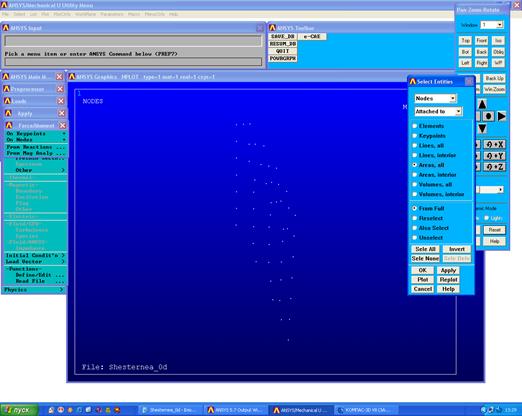
Затем, выбираем все узлы, принадлежащие этой поверхности (Select – Entities). Рисунок 9.
Рисунок 9- Вывод узлов
Нагружение зуба силой, действующей по нормали к поверхности зуба осуществляем в момент, когда она приложена к вершине зуба. Действующими по трем осям, нагрузку прикладываем к вершине зуба Main Menu→Preprocessor→Loads→Apply→Force/Moment→On Nodes. Рисунок 10.
Рисунок 10- Приложение усилий
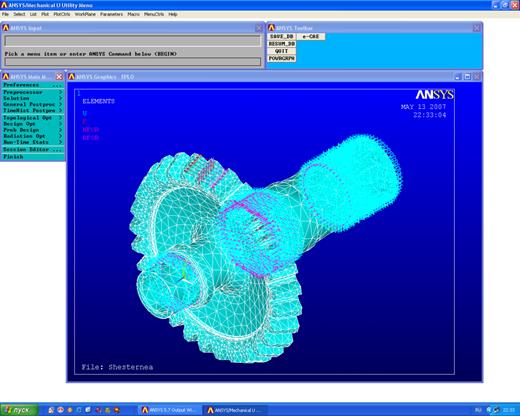
Переходим в изометрическое изображение детали Utility Menu→Select→ →Everything. Utility Menu→Plot→Volumes. Для проведения расчёта воспользуемся функцией решения Main Menu→ →Solution→Current LS. См. Рисунок 11. Для просмотра конечных результатов воспользуемся функцией просмотра результата решения Main Menu→General Postproc→Plot ResultsNodal Solution.
Рисунок 11- Нагруженное состояние шестерни
При расчете по данной методике получены следующие результаты (Рисунок12 и13).
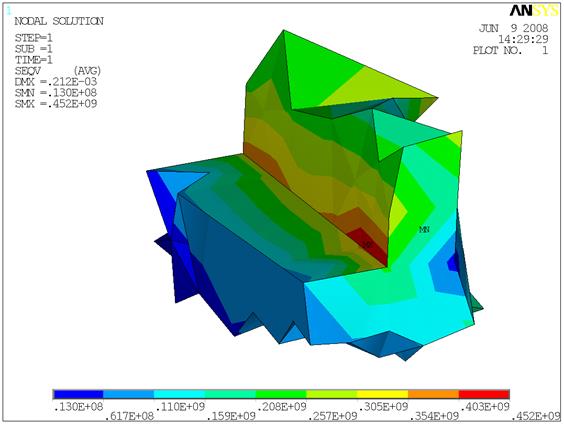
Рисунок 12 - Напряженное состояние у основания зуба
Рисунок 13- Напряженное состояние на валу в месте галтельного перехода
Из Рисунка 12 видно, что максимальные напряжения у основания зуба шестерни равны 452 МПа. Расчет методами сопротивления материалов дает 440 МПа (погрешность 2,7%). Максимальные напряжения в сечении с галтельным переходом равны 25,3 МПа. . Расчет методами сопротивления материалов дает 13,6 МПа (погрешность 46,2%).
Поиск по сайту: |
 2010
2010