 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Решение задач линейного программирования с помощью надстройки «ПОИСК РЕШЕНИЯ». ⇐ ПредыдущаяСтр 3 из 3
Надстройка «ПОИСК РЕШЕНИЯ» входит в состав электронной таблицы EXCEL. Если настройка установлена, то в меню СЕРВИС должен быть соответствующий пункт меню. В противном случае компонент легко устанавливается. Этот очень мощный математический инструмент позволяет решать задачи линейного и нелинейного программирования не требуя от пользователя почти никакой специальной подготовки.
Рассмотрим решение задачи линейного программирования с помощью этой надстройки на примере.
Найти оптимальный план производства продукции А, В, и С, максимизирующий общую прибыль при ограниченных запасах ресурсов и заданных нормах расхода этих ресурсов на производство продукции единицы продукции каждого вида.
Обозначим количество единиц продукции А, В, и С, выпускаемых предприятием, через Экономико-математическая модель этой задачи имеет такой вид:
Рассмотрим последовательность решения этой задачи средствами EXCEL. Сначала необходимо записать условие задачи на рабочем листе EXCEL. Все тексты должны быть краткими, но информативными. Например, рассматриваемая задача может быть записана так:
Для начала все компоненты плана приняты равными единице. Это не имеет значения для последующих расчетов, но удобно для проверки правильности набора формул. В колонке ЗАТРАТЫ введены формулы для расчета каждого ресурса на производство планируемого количества продукции. Так, в ячейке Ресурс1Затраты (Е4) вычислено
Теперь необходимо объяснить как набирать формулу с помощью Мастера Функций, который автоматически активизируется, как только заносим в ячейку знак равенства. Потом в раскрывающемся списке находим формулу СУММПРОИЗВ.
Щелкая по имени функции мышкой или выбирая ОК, активизируем панель ввода аргументов. В поле ввода МАССИВ 1 указываем адреса диапазона ячеек плана (протягиваем мышкой по нужному диапазону). Адреса диапазона (В10:D10) появляются в поле ввода. Прежде чем переходить к заполнению следующего поля, надо нажать F4- в записи адресов появляются фиксаторы ($B$10:$D$10). При копировании формул эти сомножители не будут изменяться (в этих ячейках находятся значения переменных
Нажимаем ОК на панели ввода или клавишу ENTER. Все остальные формулы получаются копированием. Заметим, что трудоёмкость набора формул практически не зависит ни от количества переменных, ни от количества ограничений в задаче. На следующем этапе активизируем надстройку ПОИСК РЕШЕНИЯ (меню СЕРВИС, ПОИСК РЕШЕНИЯ).
На экране появляется панель этой надстройки. Перед вызовом надстройки рекомендуется установить курсор в ячейку (ПРИБЫЛЬ ЦЕЛЬ), в которой находится значение целевой функции. В этом случае её адрес установится в поле УСТАНОВИТЬ ЦЕЛЕВУЮ ЯЧЕЙКУ. Целевую ячейку можно выбирать равной максимальному значению, минимальному значению, конкретному значению. Выбираем УСТАНОВИТЬ ЦЕЛЕВУЮ ЯЧЕЙКУ равной МАКСИМАЛЬНОМУ значению.
Далее заполняем поле ИЗМЕНЯЯ ЯЧЕЙКИ, указывая там адреса ячеек плана. Потом формулируем ограничения. Фактически у нас их два: все неизвестные – неотрицательны, и расход ресурса не превышает запаса. Не следует набирать вручную, нажимание кнопки ДОБАВИТЬ приводит к появлению панели добавление ограничения, содержащей три поля. В поле ССЫЛКА НА ЯЧЕЙКУ заносим адреса ячеек плана, в раскрывающемся списке второго поля выбираем необходимый знак ограничения. В третьем поле можно либо набрать число соответствующее правой части, либо указать адреса диапазонов такого же размера, тогда будет производиться сравнение диапазонов по компонентах.
Завершаем набор ограничений. Теперь всё готово для расчёта.
Перед нажиманием кнопки ВЫПОЛНИТЬ, полезно сперва нажать на кнопку ПАРАМЕТРЫ. Появляется панель на которой надо включить опцию ЛИНЕЙНАЯ МОДЕЛЬ. Кроме того оказывается, что требование неотрицательности компонент плана можно задать здесь, установив флажок НЕОТРИЦАТЕЛЬНЫЕ ЗНАЧЕНИЯ.
По умолчанию задано ограничение на время решения задачи, предельное число итераций и другие – этого достаточно для решения большинства задач. Однако, если, например, за указанное время оптимальное решение не будет получено, то на пенели РЕЗУЛЬТАТЫ ПОИСКА РЕШЕНИЙ появится сообщение ВРЕМЯ, УСТАНОВЛЕННОЕ ДЛЯ ПОИСКА РЕШЕНИЙ ИСТЕКЛО. ПРОДОЛЖИТЬ? При нажимании кнопки продолжить решение будет продолжаться до получения оптимального плана. Такая же ситуация с другими параметрами, установленными по умолчанию. При желании можно также поставить флажок ПОКАЗЫВАТЬ РЕЗУЛЬТАТЫ ИТЕРАЦИЙ.
Теперь нажимаем ОК, потом в появившейся панели ВЫПОЛНИТЬ. На экране появляется панель с сообщением о результатах поиска. В данном случае поиск решения завершился успешно и нам предлагают заказать три вида отчетов.
Заказываем их все, решение сохраняем, ОК.
Однако, возможна другая ситуация. Если условия задачи несовместны, то появляется сообщение ПОИСК НЕ МОЖЕТ НАЙТИ ПОДХОДЯЩЕГО РЕШЕНИЯ. Если целевая функция неограничена, то сообщение будет иметь вид ЗНАЧЕНИЯ ЦЕЛЕВОЙ ФУНКЦИИ НЕ СХОДЯТСЯ.
На следующем рисунке показан вид рабочего листа EXCEL с результатами расчёта. Итак, компоненты оптимального плана
Внизу рабочего листа видны ярлыки заказанных автоматических отчетов.
Отчёт по результатам состоит из трёх таблиц.
В первой приводятся сведения о целевой функции : её начальное значение – 83, максимальное -2050.
Во второй таблице видим исходные значения компонент плана (1; 1; 1) и полученные в результате поиска (60; 10; 0).
В третьей таблице проверяются все ограничения. В колонке ЗНАЧЕНИЕ приведены величины использованных ресурсов, в колонке РАЗНИЦА – остатки ресурсов. Если ресурс израсходован полностью, то в колонке СТАТУС указывается СВЯЗАННОЕ.
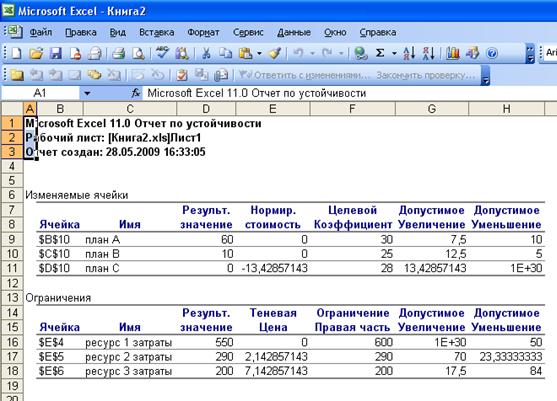
Отчёт по устойчивости состоит из двух частей.
В первой части снова приведены компоненты оптимального плана и проведен анализ устойчивости оптимального плана относительно вариации в целевых коэффициентах. Оказывается найденный план остаётся оптимальным в следующих интервалах варьирования цен В колонке НОРМИРОВАННАЯ СТОИМОСТЬ , коэффициент -13,42857143 показывает на сколько снизится прибыль при принудительном производстве единицы невыгодной продукции.
Во второй таблице проводится анализ устойчивости плана относительно вариаций в свободных членах ограничений. Указаны также теневые цены ресурсов. Например, очевидно ,что увеличение запасов недефицитного первого ресурса не приводит к увеличению прибыли.
Третий отчёт – отчёт по пределам – самый неинтересный. В нём снова приведены максимальное значение функции цели и показано, что будет, если в оптимальном плане по очереди каждую компоненту приравнять к наименьшему значению насколько позволяют ограничения.
ЛИТЕРАТУРА
Поиск по сайту: |
и 
соответственно.
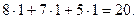Табличный курсор стоит в этой ячейке, поэтому её содержимое отображается на панели формул. Если одна формула набрана, то остальные формулы в столбце ЗАТРАТЫ получаются копированием. Справа внизу активной ячейки виден маленький квадратик. Надо схватить его мышкой и протянуть на оставшийся диапазон. В ячейке ПрибыльЦель набрана такая же формула.
и максимальное значение прибыли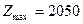 
у.е. Второй и третий ресурс израсходованы полностью, первый же ресурс остаётся неизрасходованным в количестве 50 единиц. Таким образом, распечатка финального листа EXCEL даёт понятный и полный отчет о решении задачи.
.
