 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Понятие линейного программирования.Стр 1 из 3Следующая ⇒
ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД УНІВЕРСИТЕТ ЕКОНОМІКИ ТА ПРАВА "КРОК" ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ КОНСПЕКТ ЛЕКЦИЙ ДЛЯ СТУДЕНТОВ ИНОСТРАНЦЕВ Составитель МАЦЮК Л.В. Содержание 1. Предмет математического программирования. 2. Экономико-математические модели. Основные понятия, термины и определения. 3. Понятие линейного программирования. 4. Примеры задач линейного программирования. 5. Геометрическая интерпретация задач линейного программирования. Графический метод. 6. Решение задач линейного программирования с помощью надстройки «ПОИСК РЕШЕНИЯ».
Предмет математического программирования Исследование операций – это наука, изучающая проблемы управления экономическими системами, оптимизации их структуры, развития и функционирования с целью получения максимальной экономической эффективности. Математическое программирование – это один из инструментов теории исследования операций.
Математическое программирование – это математическая дисциплина, в которой разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах математического программирования оказываются непригодными. Для решения задач математического программирования разработаны и разрабатываются специальные методы и теории. Так как при решении этих задач приходится выполнять значительный объем вычислений, то при сравнительной оценке методов большое значение придается эффективности и удобству их реализации на ЭВМ. Началом развития математического программирования как самостоятельного научного направления следует считать первые попытки использования методов решения оптимизационных задач в прикладных исследованиях, в первую очередь в экономике. Следует отметить важную роль российского ученого Л.В.Канторовича, который в конце 30-х годов сформулировал и исследовал основные задачи, критерии оптимальности, методы решения и геометрическая интерпретация результатов решения задач линейного программирования. В 1939 году была опубликована монография Л.В.Канторовича «Математические методы организации и планирования производства». В 1941 году американский ученый Хичкок разработал постановку транспортной задачи. Термин “линейное программирование” ввели позже американские ученые Дж.Данциг и Г.Кумпанс. В 1947-1949 годах Дж.Данциг разработал также основной метод решения задач линейного программирования - симплекс метод, появление которого выделяет линейное программирование как самостоятельное направление в математическом программировании. Термин "программирование" в названии дисциплины ничего общего с термином "программирование (т.е. составление программы) для ЭВМ" не имеет, т.к. дисциплина "линейное программирование" возникла еще до того времени, когда ЭВМ стали широко применяться для решения математических, инженерных, экономических и др. задач. Термин "линейное программирование" возник в результате неточного перевода английского "linear programming". Одно из значений слова "programming" - составление планов, планирование. Следовательно, правильным переводом английского "linear programming" было бы не "линейное программирование", а "линейное планирование", что более точно отражает содержание дисциплины. Однако, термины линейное программирование, нелинейное программирование, математическое программирование и т.д. в нашей литературе стали общепринятыми. Экономико-математические модели. Основные понятия, термины и определения. Любое планирование начинается с изучения и постановки задачи. На этом этапе необходимо выделить важные и существенные сведения и обросить все второстепенное и случайное. Иными словами надо составить модель экономической ситуации. Математическая модель заключается в адекватном переводе всех существенных сведений о решаемой проблеме на на язик математики в виде уравнений, функций и неравенств. В зависимости от вида этих соотношений все задачи математического программирования делятся на два основных класса:
Если все соотношения– линейные функции, то соответствующая задача поиска экстремума является задачей линейного программирования. Если хотя бы одна из указанных функций нелинейная, то соответствующая задача поиска экстремума является задачей нелинейного программирования.
Составление математической модели увлекательная задача, требующая понимания сути экономических процессов, опыта. В данной ситуации чрезмерное упрощение как и чрезмерное усложнение (принятие во внимание несущественных факторов) не всегда приводят к моделям адекватно описывающим практическую задачу и соответственно не всегда позволяют получить решения полезные с практической точки зрения. С этой точки зрения, экономико-математическое моделирование – это искусство, основывающееся на знаниях, опыте, интуиции.
Современная компьютерная техника значительно упрощает решение задач математического программирования. Необходимо умение использовать готовые программные средства, например, надстройку “Поиск решения”, которая входит в состав электронной таблицы Excel. Тем не менее, умение разбираться в вопросах математического моделирования и методах оптимизации, методах анализа полученных решений есть важное условие успешного решения задач математического программирования.
Можно выделить следующие этапы решения задачи математического программирования:
- анализ проблемной ситуации, чёткая формулировка цели исследования;
- построение экономико-математической модели;
- выбор методов решения и необходимых программных средств;
- правильная подготовка данных и решение задачи;
- анализ полученных результатов, определение возможностей их использования.
Экономико- математическая модель состоит из целевой функции, максимум или минимум которой необходимо найти, и системы ограничений, имеющей вид неравенств или равенств и характеризующей конкретную экономическую задачу.
Cистема соотношений (1)-(3) –экономико-математическая модель экономической системы.
Совокупность чисел
Допустимый план
Понятие линейного программирования. Итак, линейное программирование возникло после второй мировой войны и стало быстро развиваться, привлекая внимание математиков, экономистов и инженеров благодаря возможности широкого практического применения, а также математической стройности. Линейное программирование применяется при решении экономических задач, в таких задачах как управление и планирование производства; в задачах определения оптимального размещения оборудования на морских судах, в цехах; в задачах определения оптимального плана перевозок груза (транспортная задача); в задачах оптимального распределения кадров и т.д. Задача линейного программирования (ЛП), как уже ясно из сказанного выше, состоит в нахождении минимума (или максимума) линейной функции при линейных ограничениях. Общая форма задачи имеет вид: найти
при условиях
где
Cистема соотношений (1')-(3') –общий вид задачи линейного программирования. Ограничения (3') называют условиями неотрицательности переменных. В рассматриваемом случае все ограничения имеют вид неравенств. Иногда они могут быть смешанными, то есть неравенства и равенства. Если все ограничения (2') имеют вид строгих равенств
где
Совокупность чисел
Допустимый план
Поиск по сайту: |
 (1)
(1) (2)
(2)
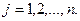 (3)
(3) удовлетворяющих ограничениям (2), (3) называется допустимым планом (решением) задачи математического программирования.
удовлетворяющих ограничениям (2), (3) называется допустимым планом (решением) задачи математического программирования. при котором целевая функция (1) принимает своё максимальное (минимальное) значение называется оптимальным.
при котором целевая функция (1) принимает своё максимальное (минимальное) значение называется оптимальным. (1')
(1') (2')
(2') (3')
(3') (2'')
(2'') неотрицательны, то данная форма записи называется канонической.
неотрицательны, то данная форма записи называется канонической. удовлетворяющих ограничениям (2'), (3') называется допустимым планом (решением) задачи линейного программирования. Множество допустимых планов представляет собой выпуклое многогранное множество или выпуклый многогранник.
удовлетворяющих ограничениям (2'), (3') называется допустимым планом (решением) задачи линейного программирования. Множество допустимых планов представляет собой выпуклое многогранное множество или выпуклый многогранник.