|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Представление сигнала при амплитудной модуляции в частотной области
Если модулирующий сигнал является периодическим, его можно разложить в ряд Фурье. Пусть подавляющая часть энергии этого сигнала содержится в N гармониках, тогда
Подставляя это выражение в формулу для модулированного сигнала получим mi - коэффициент амплитудной модуляции. Рис 1.3 иллюстрирует преобразование спектра первичного сигнала в случае N = 3 (а) и соответствующий спектр сигнала при АМ (б).
а) б) Рисунок 1.3. – Преобразование спектра модулирующего колебания (а) в спектр модулированного колебания (б) Модулирующее колебание может быть и дискретной функцией времени. Так на рис.1.4. показана эпюра напряжения при модуляции несущей прямоугольными импульсами (радиоимпульсы).
Рисунок 1.4. – Эпюра и спектр радиоимпульса Линейчатый спектр импульсной последовательности исходного сигнала при модуляции сдвигается из низкочастотной области в высокочастотную на частоту несущего колебания f0. В пределе, если спектр Uс(t)является сплошным в диапазоне от fн до fв, в спектре АМ содержится несущая и две сплошные боковые полосы, при этом форма нижней боковой зеркальна по отношению к форме верхней боковой. Рассмотренный вид амплитудной модуляции является так называемой полной амплитудной модуляцией, так как в спектре содержатся несущее колебание и обе боковые полосы. Вместе с тем информация о передаваемом сообщении не содержится в составляющей на несущей частоте. Энергетически выгоднее подавить несущую и одну боковую составляющую. На приемной стороне без потери можно восстановить первичный сигнал. Энергия амплитудно-модулированного колебания за период определяется как
Из этого выражения видно, что мощность сигнала с АМ за период Т состоит из мощности колебания на частоте w0 модулируемого сигнала Р0 и мощности
На составляющую модулируемого колебания Рw (не переносящую информации!) на частоте w, при ma=1 тратится бесполезно большая часть энергии, она составляет
На боковые составляющие приходится только третья часть всей мощности, то есть
следовательно, сигнал с амплитудной модуляцией энергетически невыгоден. Кроме того, ширина его спектра DFс в два раза больше ширины спектра модулирующего сигнала и определяется как DFс = 2Fм, где Fм – максимальная частота модулирующего сигнала. Балансная модуляция Для более эффективного использования мощности передатчика можно формировать АМ сигналы с подавленной несущей. Такая модуляция называется балансной. Балансно-модулированное колебание можно получить двояким способом. При первом способе полное АМ подается на частотный фильтр, который подавляет частотную составляющую на f0 . Второй более распространенный способ основан на использовании схемы модулятора, отображенного на рис.1.5.
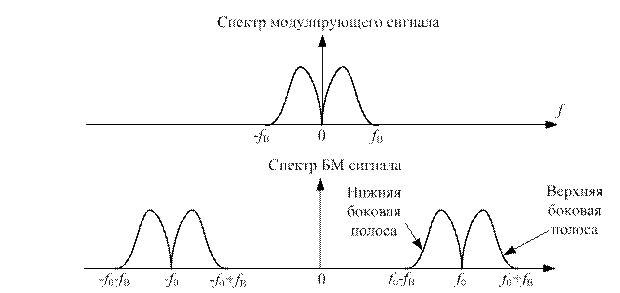
Рисунок 1.5.- Схема модулятора Спектр первичного сигнала обычно расположен в ограниченном диапазоне низких частот DFc = fН ¸ fВ. Спектр БМ сигнала UБМ(t) = Uм(t)cos w0t можно найти, используя свойства преобразования Фурье. В соответствии с этим свойством, если Таким образом, в результате перемножения получаются две боковые полосы без несущей. Эпюра напряжения БМ сигнала показана на рис. 1.6, спектр - на рис. 1.7. Огибающая БМ положительна по определению и равна |Uc(t)|. При гармоническом законе модуляции Uм(t) = Uм cos(WMt) ипри единичной амплитуде несущего колебания напряжение на выходе балансного модулятора равно
Рисунок 1.6. – Эпюра сигнала при БМ
Рисунок 1.7. – Спектры балансно-модулированнных сигналов. Балансная модуляция позволяет более рационально распределить энергию колебания, однако, ширина спектра остается такой же, как и при АМ. Симметрия спектра означает, что верхняя боковая полоса частот (ВБП) и
Поиск по сайту: |
 .
. ;
;

 .
. , приходящейся на боковые составляющие, то есть
, приходящейся на боковые составляющие, то есть .
. .
. ,
,
 соответствует спектр
соответствует спектр  , то сигналу
, то сигналу  соответствует спектр
соответствует спектр  .
.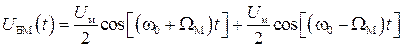 .
.