 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Аналитическое выражение амплитудно-модулированного колебанияСтр 1 из 4Следующая ⇒
ЛАБОРАТОРНАЯ РАБОТА № 1
ИССЛЕДОВАНИЕ ГАРМОНИЧЕСКИХ СИГНАЛОВ РАЗЛИЧНОЙ МОДУЛЯЦИЕЙ
Цель работы: исследование временного и спектрального представления модулированных сигналов при разных видах сообщения в виде гармонического сигнала, последовательности прямоугольных импульсов, гаусовского случайного сигнала и при разных видах модуляции гармонического несущего сигнала. Подготовка к выполнению работы Во время подготовки необходимо изучить теоретический материал по конспекту лекций, рекомендованной литературе и приведенными ниже краткими теоретическими сведениями. При подготовке особое внимание нужно уделить преобразованию сигналов во временной и спектральной области при различных видах модуляции. Изобразить спектры сигналов для АМ и ЧМ модуляции для модулирующего гармонического сигнала. Модулированные сигналы Следует различать модуляцию различных уровней: - первичного, когда осуществляется преобразование исходного сигнала в более удобную форму (АИМ, ШИМ); - вторичного, когда информационный или преобразованный сигнал переводится в область высоких частот для передачи его в линию связи. В системах передачи информации первичные сигналы, полученные путем первичного преобразования сообщений, являются непригодными для непосредственной передачи по линиям связи. Необходим перенос первичных сигналов из низкочастотной области в область частот, соответствующую среде распространения в линии связи. Различаются следующие виды модуляции: - непрерывная (аналоговая) модуляция; - импульсная модуляция; - цифровая модуляция. При непрерывной модуляции переносчиком, или несущим колебанием, является высокочастотное гармоническое колебание. При импульсной модуляции переносчиком является периодическая последовательность прямоугольных импульсов. Цифровой модуляцией называют преобразование квантованного сигнала в кодограммы. В современных системах передачи используется сочетание различных видов модуляции. Амплитудная модуляция гармонического несущего колебания Аналитическое выражение амплитудно-модулированного колебания При амплитудной модуляции (AM) измененяемым по закону первичного сигнала ( модулируемым ) параметром несущего колебания является его амплитуда. Получаемое модулированное колебание имеет вид
где Частота w0 и фаза несущей остаются неизменными. В общем случае функция U0(t) может быть как непрерывной, так и дискретной и является огибающей модулированного сигнала. При амплитудной модуляции огибающую можно представить как
mа=aАМ/U0- коэффициент амплитудной модуляции (глубина модуляции). Временные диаграммы амплитудно-модулированного колебания (АМ) приведены на рис. 1.1.
Рисунок 1.1. – Эпюры АМ, для произвольного модулирующего сигнала В случае гармонического модулирующего сигнала
где Wm - частота модулирующего сигнала, Uм - амплитуда модулирующего колебания, U0 - амплитуда несущей, mа=aUm/U0.
или
Очевидно, что спектр АМ сигнала в этом случае представляет собой сумму 3-х гармонических колебаний с частотами w0, w0 + WМ, w0 - WМ . Спектральная диаграмма для амплитуд гармоник показана на рис. 1.2. Первое слагаемое в выражении - несущее колебание. Ему соответствует на графике составляющая на частоте w0. Второе слагаемое - гармоника с частой w0 + WМ образует верхнюю боковую составляющую спектра, слагаемое с частотой w0 - WМ образует нижнюю боковую.
Рисунок 1.2. – Спектр сигнала при амплитудной модуляции
Поиск по сайту: |
 ,
, - изменяет уровень под действием модулирующего сигнала.
- изменяет уровень под действием модулирующего сигнала. ,
,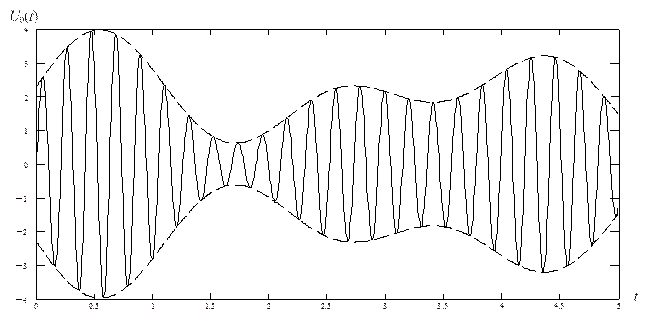
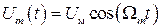 ,
,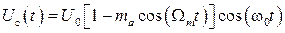 ,
,

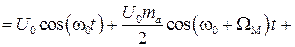
 .[*]
.[*]