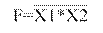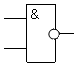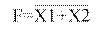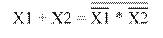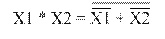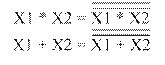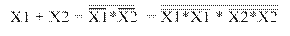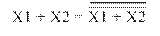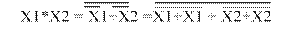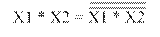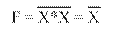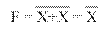|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Реализация цифровых схем на базовых ЛЭ
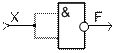
В цифровой электронике имеется набор ЛЭ, реализующих функции, с помощью которых могут быть получены все остальные функции булевой алгебры (конъюнкция, дизъюнкция, инверсия). К таким элементам относятся элементы И-НЕ и ИЛИ-НЕ имеющие по 2 входа. Эти элементы называются базовыми. Базовый ЛЭ И-НЕявляется комбинацией ЛЭ И и НЕ.
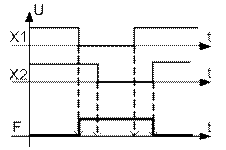
На выходе базового ЛЭ И-НЕ (рисунок 1.4) сигнал уровня 0 будет в том случае, когда на всех его входах присутствует сигнал уровня 1.
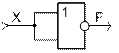
Базовый ЛЭ ИЛИ-НЕ является комбинацией ЛЭ ИЛИ и НЕ.
На выходе базового ЛЭ ИЛИ-НЕ (рисунок 1.5) сигнал уровня 1 будет только в том случае, когда на обоих его входах присутствует сигнал уровня 0.
Схемотехнически любая цифровая схема может быть выполнена только на базовом ЛЭ И-НЕ, или только на базовом ЛЭ ИЛИ-НЕ. Для приведения логического выражения к базовому ЛЭ И-НЕ или базовому ЛЭ ИЛИ-НЕ используются первая и вторая теоремы Де-Моргана, правило двойного отрицания и правило повторения.
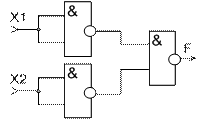
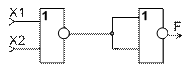
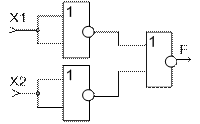
Преобразование функции ИЛИ к базовому ЛЭ И-НЕ осуществляется с помощью теоремы Де-Моргана (рисунок 1.6.а). Преобразование функции ИЛИ к базовому ЛЭ ИЛИ-НЕ осуществляется согласно правилу двойного отрицания (рисунок 1.6.б).
Преобразования функции И к базовым ЛЭ ИЛИ-НЕ и И-НЕ представлены на рисунке 1.7.
Функция НЕ реализуется на базовом ЛЭ И-НЕ или базовом ЛЭ ИЛИ-НЕ объединением их входов с использованием соответствующего правила повторения. Преобразования функции НЕ (инверсия) к базовому ЛЭ И-НЕ и базовому ЛЭ ИЛИ-НЕ представлены на рисунке 1.8.
Поиск по сайту: |