Арифметические устройства

Комбинационные устройства, которые рассматривались до сих пор, выполняют логические функции. Входные и выходные сигналы высокого и низкого уровня оцениваются соответственно как логическая “1” и логический “0”.

Дискретная техника оперирует и другим классом устройств, назначение которых состоит в выполнении арифметических действий с двоичными числами.

Особенность арифметических устройств состоит в том, что сигналам приписываются не логические, а арифметические значения 1 и 0 и действия над ними подчиняются законам двоичной арифметики. Для описания их работы также удобно пользоваться таблицами истинности.

Важнейшая из арифметических операций – сложение ( суммирование ). Помимо прямого назначения она используется и при других операциях: вычитание – это сложение, в котором вычитаемое вводится в обратном или дополнительном коде, а умножение и деление – это последовательное сложение и вычитание. К арифметическим устройствам относят также узлы, выполняющие специальные операции, как то: сравнение двух чисел и выявление четности заданных чисел (определение паритета ).

Сумматоры

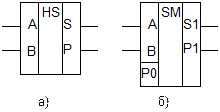
Простейшим суммирующим элементом является полусумматор. Он имеет два входа А и В и два выхода: S (cумма ) и P (перенос) (рис. 3.11,а).

Рис. 3.11. Суммирующие элементы

Процедуру сложения двух n – разрядных двоичных чисел можно представить следующим образом. Сложение цифр А0 и В0 младшего разряда дает бит суммы S0 и бит переноса P1. В следующем разряде производится сложение цифр А1, В1, и Р1, которое формирует бит суммы S1 и перенос Р2.

Полный одноразрядный сумматор имеет три входа (рис.3.11,б): два для слагаемых А и В и один для сигнала переноса с предыдущего разряда.

На рис. 3.12 показана схема, поясняющая принцип действия n- разрядного сумматора с последовательным переносом. Число сумматоров здесь равно числу разрядов. Выход переноса Р каждого сумматора соединен со входом переноса следующего, более старшего разряда. На входе переноса сумматора младших разрядов установлен “0”, так как сигнал переноса сюда не поступает.

Рис. 3.12 Сумматор с последовательным переносом.

Слагаемые А _i и B_i складываются во всех разрядах одновременно, а перенос Р поступает с окончанием операции сложения в предыдущем разряде.

Быстродействие многоразрядных сумматоров подобного вида ограничено задержкой переноса, так как формирование сигнала переноса на выходе старшего разряда не может произойти до тех пор, пока сигнал переноса младшего разряда не распространится последовательно по всей схеме.

Время переноса можно уменьшить, вводя параллельный перенос, для чего применяют специальные узлы – блоки ускоренного переноса. Они имеют достаточно сложную схему даже для n = 4 и с увеличением числа разрядов сложность настолько возрастает, что изготовление их становится нецелесообразно.

В виде отдельных микросхем выпускаются одноразрядные, двухразрядные и четырехразрядные сумматоры. В семействе ТТЛ это микросхемы соответственно К155ИМ1, ИМ2 и ИМ3.

Цифровые компараторы

Цифровые компараторы (от compare - сравнивать) выполняют сравнение двух чисел, заданных в двоичном ( двоично-десятичном ) коде.

Простейшие компараторы формируют на выходе однобитовый сигнал равенства – “1” или неравенства - “0” двух чисел. Более сложные компараторы в случае неравенства определяют, которое из чисел больше.

Пример. Построить на ЛЭ схему сравнения на равенство двух 8-разрядных чисел.

Особенность задачи в том, что для ее решения практически невозможно построить таблицу: число строк в ней будет 2⁽⁸⁺⁸⁾ = 65536. Подобные задачи решают иначе – методом декомпозиции задачи - разбиения ее на более мелкие подзадачи. В нашем случае: два числа равны, если попарно равны их одноименные разряды. Структурная схема компаратора показана на рис. 3.13, а. Известно, что функция равенства двух аргументов – это инверсия их суммы по модулю 2. Чтобы исключить из проектируемой схемы 8 инверторов воспользуемся соотношением:

Рис. 3.13 Узел сравнения на равенство.

Это решение показано на рис. 3.13,б. Оно учитывает, что в семействах ЛЭ нет элемента 8ИЛИ - НЕ, а есть только 4ИЛИ – НЕ.

Примером компаратора, определяющего знак неравенства, может служить 4-разрядная микросхема К555СП1. Она имеет три выхода: ”A>B”, “А=В” и “A<B”, и в зависимости от соотношения А и В активный уровень появляется на одном из этих выходов. Входы “>”,”<”,”=” служат для наращивания разрядности.

Рис.3.14 Компаратор К555СП1.

Контроль четности

На передаваемые по линии связи или хранимые в памяти данные воздействуют различные помехи, которые могут исказить эти данные. Простейшим способом удостовериться, что данные искажены ошибкой, служит введение контроля по четности (parity check). В его основе лежит операция сложения по модулю 2 всех двоичных разрядов контролируемого слова. Если число единиц в слове четное, то сумма по модулю 2 его разрядов будет “0”, если нечетное то “1”. Признаком четности называют инверсию этой суммы.

Реализация этого метода осуществляется с помощью специальных схем контроля четности, которые выпускаются в микросхемном исполнении.

На основе информации на выходе передающего устройства такая схема формирует дополнительный бит (1 или 0), так называемый паритетный или контрольный бит (parity bit), который добавляется к выходной информации. Назначение этого бита - доводить число единиц в каждом передаваемом слове до четного или не четного в зависимости от принятой системы кодирования. При всех передачах информации, включая запись в память, контрольный бит передается вместе с n-разрядным словом.

На приемном конце линии или после чтения из памяти от полученного (n+1)-разрядного слова снова берется свертка его четности. Если паритет поступившего слова правилен, разрешается прием. Если нет, то или в передаваемом слове, или в контрольном разряде при передаче или хранении произошла ошибка. Столь простой контроль не позволяет исправить ошибку, но он дает возможность при обнаружении ошибки исключить неверные данные, затребовать повторную передачу и т.д.

На практике чаще используется нечетный паритет. Контроль нечетности позволяет фиксировать полное пропадание информации, т.к. слово из одних нулей (включая контрольный бит) противоречит нечетному паритету.

Конроль по четности основан на том, что одиночная ошибка ( безразлично пропадание еденици или появление лишней ) инвертирует бит паритета. Однако две ошибки проинвертируют его дважды, поэтому двойную ошибку контроль по четности не обнаруживает. Очевидно, что контроль по четности обнаруживает все нечетные ошибки и не реагирует на любые четные. Пропуск четных ошибок - это следствие предельно малой избыточности контроля, равной всего одному разряду. Для более глубокого контроля требуется соответственно и большая избыточность.

Если ошибки взаимно независимы, то из необнаруживаемых чаще всего будет встречаться двойная ошибка. При вероятности одиночной ошибки равной q, вероятность двойной будет q². Поскольку в цифровых устройствах q<<1, не обнаруженные двойные ошибки встречаются значительно реже, чем обнаруженные одиночные. Поэтому даже при таком простом контроле качество работы устройства существенно возростает. В ответственных случаях для выявления и коррекции ошибок применяют специальные методы кодирования.

Поиск по сайту: